题目内容
4．已知关于x的方程kx2+（2k-5）x+k=0有两个实数根，求k的取值范围．分析 根据一元二次方程的定义和判别式的意义得到k≠0且△=（2k-5）2-4k•k≥0，然后求出两个不等式的公共部分即可．
解答 解：根据题意得k≠0且△=（2k-5）2-4k•k≥0，
所以k≤$\frac{5}{4}$且k≠0．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
全优点练单元计划系列答案
相关题目
14．如果一个多边形的外角分别是10°，20°，30°…，那么这个多边形是（ ）
| A． | 六边形 | B． | 七边形 | C． | 八边形 | D． | 九边形 |
如图是一个物体的三视图，根据图中尺寸（单位：cm），它的体积为32+8πcm3．
19．
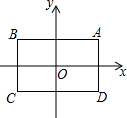如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）
如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）| A． | $\frac{3}{4}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | $\frac{3}{2}$ |
19．
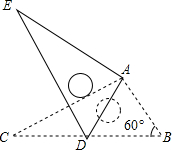如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=1，∠B=60°，则△ABD的面积为（ ）
如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=1，∠B=60°，则△ABD的面积为（ ）| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{4}$ |