题目内容
如图，在△ABC中，ED交AB于E，交AC于D，| AD |
| AB |
| AE |
| AC |
| 3 |
| 5 |
考点：相似三角形的判定与性质
专题：
分析：如图，设△ABC的周长与△ADE的周长分别为λ、μ；首先证明△ABC∽△ADE，得到
=
=
；结合λ-μ=16求出λ、μ，即可解决问题．
| λ |
| μ |
| AB |
| AD |
| 5 |
| 3 |
解答：解：如图，设△ABC的周长与△ADE的周长分别为λ、μ；
∵
=
=
，且∠A=∠A，
∴△ABC∽△ADE，
=
=
，
∴3λ-5μ=0①；由题意得：λ-μ=16②，
联立①②并解得：λ=40，μ=24．
即△ABC和△ADE的周长分别为40，24．
解：如图，设△ABC的周长与△ADE的周长分别为λ、μ；∵
| AD |
| AB |
| AE |
| AC |
| 3 |
| 5 |
∴△ABC∽△ADE，
| λ |
| μ |
| AB |
| AD |
| 5 |
| 3 |
∴3λ-5μ=0①；由题意得：λ-μ=16②，
联立①②并解得：λ=40，μ=24．
即△ABC和△ADE的周长分别为40，24．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；应牢固掌握相似三角形的判定及其性质，数形结合，准确运用相似三角形的判定及其性质来分析、解答．
练习册系列答案
相关题目
2014年巴西世界杯是第20届世界杯足球赛，比赛于2014年6月12日至7月13日在南美洲国家巴西境内举行．给全世界足球爱好者带来了一场足球盛宴．足球一般是有黑白两种颜色的皮块缝制而成，如图所示，黑色皮块是正五边形，白色皮块是正六边形，若一个球上共有黑白皮块32块，请你计算一下，黑色皮块和白色皮块的块数依次为（ ）| A、16块、16块 |
| B、8块、24块 |
| C、20块、12块 |
| D、12块、20块 |
求阴影部分的面积．（取π=3）
如图，在△ABC中，D是AB边上一点，且AD：DB=5：3，过点D作DE∥BC，交边AC于点E，那么ED用BC可表示为
如图，四边形ABCD中，∠C=75°，∠D=120°，cosB=
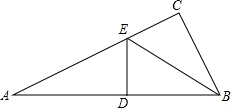如图，把Rt△ABC（∠C=90°）折叠，使A、B两点重合，得到折痕ED，再沿BE折叠，C点恰好与D点重合，则∠A等于（ ）| A、45° | B、30° |
| C、60° | D、20° |