题目内容
已知x+
=3,求x2+
的值.
(1)一变:已知x+
=3,求x4+
的值;
(2)二变:已知x2-3x+1=0,求x4+
的值.
| 1 |
| x |
| 1 |
| x2 |
(1)一变:已知x+
| 1 |
| x |
| 1 |
| x4 |
(2)二变:已知x2-3x+1=0,求x4+
| 1 |
| x4 |
考点:分式的混合运算,完全平方公式
专题:
分析:(1)先求出x2+
=(x+
)2-2=7,再得出x4+
=(x2+
)2-2=47即可;
(2)由x2-3x+1=0,变形为x+
=3,再同(1)求出结果.
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x4 |
| 1 |
| x2 |
(2)由x2-3x+1=0,变形为x+
| 1 |
| x |
解答:解:(1)∵(x+
)2=x2+2+
,
∴x2+
=(x+
)2-2=32-2=7,
∴x4+
=(x2+
)2-2
=72-2
=47;
(2)∵x2-3x+1=0,
∴x+
=3,
∴x2+
=(x+
)2-2=32-2=7,
∴x4+
=(x2+
)2-2=72-2=47.
| 1 |
| x |
| 1 |
| x2 |
∴x2+
| 1 |
| x2 |
| 1 |
| x |
∴x4+
| 1 |
| x4 |
| 1 |
| x2 |
=72-2
=47;
(2)∵x2-3x+1=0,
∴x+
| 1 |
| x |
∴x2+
| 1 |
| x2 |
| 1 |
| x |
∴x4+
| 1 |
| x4 |
| 1 |
| x2 |
点评:本题考查了分式的混合运算以及完全平方式;运用完全平方式进行变形计算是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
将?ABCD绕O点旋转到?A′B′C′D′的位置,错误的是( )
| A、AB=A′B′ |
| B、AB一定平行于A′B′ |
| C、∠B=∠B′ |
| D、△ABC≌△A′B′C′ |
 如图,已知AB∥CD,BE平分∠ABD,DE平分∠CDB,求证:BE⊥DE.
如图,已知AB∥CD,BE平分∠ABD,DE平分∠CDB,求证:BE⊥DE. 如图,点A,O,D在同一条直线上,△OAB≌△OCD,且AD=5cm,OC═3cm,∠AOC=70°,求OB的长及∠BOD的度数.
如图,点A,O,D在同一条直线上,△OAB≌△OCD,且AD=5cm,OC═3cm,∠AOC=70°,求OB的长及∠BOD的度数.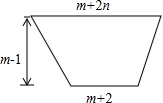 如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值.
如图所示,一条水渠的横截面是一个下窄上宽的梯形,河底宽(m+2)米,渠宽(m+2n)米,求表示水渠横截面面积S的代数式,并求出当m=4,n=0.5时S的值. 如图,在△ABC中,ED交AB于E,交AC于D,
如图,在△ABC中,ED交AB于E,交AC于D,