题目内容
 如图,四边形ABCD中,∠C=75°,∠D=120°,cosB=
如图,四边形ABCD中,∠C=75°,∠D=120°,cosB=| 3 |
| 5 |
| 3 |
考点:解直角三角形
专题:计算题
分析:作AE⊥BC于E,作AF⊥CD于F,连结CA,如图,先在Rt△ADE中根据含30度的直角三角形三边的关系计算出DF、AF,于是可判断△FAC为等腰直角三角形,所以∠ACF=45°,AC=
AF=2
,这样可得∠ACE=30°,接着在Rt△ACE中,计算出AE,然后在Rt△ABE中,利用勾股定理和锐角三角函数求AB的长.
| 2 |
| 6 |
解答:解:作AE⊥BC于E,作AF⊥CD于F,连结CA,如图,
∵∠D=120°,
∴∠ADE=60°,
在Rt△ADE中,∵∠DAE=30°,
∴DF=
AD=2,
AF=
FD=2
,
∴FC=DF+DC=2+2
-2=2
,
∴FA=FC,
∴△FAC为等腰直角三角形,
∴∠ACF=45°,AC=
AF=2
,
∵∠C=75°,
∴∠ACE=30°,
在Rt△ACE中,AE=
AC=
,
在Rt△ABE中,cosB=
=
,
设BE=3x,AB=5x,
∴AE=
=4x,
∴4x=
,解得x=
,
∴AB=5x=
.

∵∠D=120°,
∴∠ADE=60°,
在Rt△ADE中,∵∠DAE=30°,
∴DF=
| 1 |
| 2 |
AF=
| 3 |
| 3 |
∴FC=DF+DC=2+2
| 3 |
| 3 |
∴FA=FC,
∴△FAC为等腰直角三角形,
∴∠ACF=45°,AC=
| 2 |
| 6 |
∵∠C=75°,
∴∠ACE=30°,
在Rt△ACE中,AE=
| 1 |
| 2 |
| 6 |
在Rt△ABE中,cosB=
| BE |
| AB |
| 3 |
| 5 |
设BE=3x,AB=5x,
∴AE=
| AB2-BE2 |
∴4x=
| 6 |
| ||
| 4 |
∴AB=5x=
5
| ||
| 4 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.合理作辅助线是解决此题的关键.

练习册系列答案
相关题目
将?ABCD绕O点旋转到?A′B′C′D′的位置,错误的是( )
| A、AB=A′B′ |
| B、AB一定平行于A′B′ |
| C、∠B=∠B′ |
| D、△ABC≌△A′B′C′ |
 如图,在△ABC中,ED交AB于E,交AC于D,
如图,在△ABC中,ED交AB于E,交AC于D,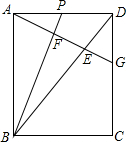 如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
如图,在矩形ABCD中,P是AD上一动点,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G. 如果两个角的差的绝对值等于90°,就称这两个角互为反余角,其中一个角叫做另一个角的反余角.例如:∠1=120°,∠2=30°,∠1-∠2=90°,则∠1和∠2互为反余角,其中∠1是∠2的反余角,∠2也是∠1的反余角.
如果两个角的差的绝对值等于90°,就称这两个角互为反余角,其中一个角叫做另一个角的反余角.例如:∠1=120°,∠2=30°,∠1-∠2=90°,则∠1和∠2互为反余角,其中∠1是∠2的反余角,∠2也是∠1的反余角.