题目内容
7. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 利用勾股定理求出AB的长度,然后根据sinB=$\frac{AC}{AB}$代入数据进行计算即可得解.
解答 解:∵∠C=Rt∠,AC=4,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴sinB=$\frac{AC}{AB}$=$\frac{4}{5}$.
故选D.
点评 本题考查了锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
17.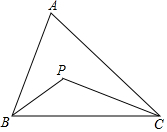 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )| A. | 102° | B. | 112° | C. | 115° | D. | 118° |
18.如果多项式y2+my+16是完全平方式,那么m的值为( )
| A. | 8 | B. | -8 | C. | ±4 | D. | ±8 |
15.北国超市的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=-20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量•(售价-进价)]( )
| A. | 5元 | B. | 4元 | C. | 3.5元 | D. | 3元 |
2. 如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
 如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )| A. | 130° | B. | 65° | C. | 35° | D. | 25° |
12. 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )| A. | $4\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
19.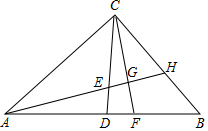 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )
 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )| A. | 2 | B. | π | C. | 2 | D. | $\frac{{\sqrt{2}}}{2}$π |
16.在一次函数y=-x+2的图象上的点是( )
| A. | (-1,4) | B. | (2,0) | C. | (1,0) | D. | (2,1) |
17.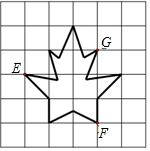 如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )
如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )
 如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )
如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )| A. | (1,2) | B. | (2,2) | C. | (2,1) | D. | (1,1) |