题目内容
3.下列从左到右变形正确的是( )| A. | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B. | $\frac{{x-\frac{1}{2}y}}{{\frac{1}{2}x+y}}=\frac{2x-y}{x+2y}$ | ||
| C. | $-\frac{x+1}{x-y}=\frac{x-1}{x-y}$ | D. | $\frac{a+b}{a-b}=\frac{a-b}{a+b}$ |
分析 A、分子分母同时乘以10,分子的b和分母的a漏乘,所以不正确;
B、分子分母同时乘以2,正确;
C、把负号放在分子上,x没有变号,不正确;
D、当a+b=a-b时才相等.
解答 解:A、$\frac{0.2a+b}{a+0,2b}$=$\frac{10×(0.2a+b)}{10×(a+0.2b)}$=$\frac{2a+10b}{10a+2b}$,所以选项A变形不正确;本选项不符合题意
B、$\frac{x-\frac{1}{2}y}{\frac{1}{2}x+y}$=$\frac{2×(x-\frac{1}{2}y)}{2×(\frac{1}{2}x+y)}$=$\frac{2x-y}{x+2y}$,所以选项B变形正确;本选项符合题意,
C、-$\frac{x+1}{x-y}$=$\frac{-x-1}{x+y}$,所以选项C变形不正确;本选项不符合题意,
D、$\frac{a+b}{a-b}$$≠\frac{a-b}{a+b}$,所以选项D变形不正确;本选项不符合题意,
故选B.
点评 本题考查了分式的基本性质,熟练掌握分式的基本性质是关键,注意理解分子和分母要同时乘或除一个不为0的数或式子,分式的值不变.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
11.下面式子从左边到右边的变形是因式分解的是( )
| A. | x2-x-2=x(x-1)-2 | B. | (x+1)(x-1)=x2-1 | C. | x2-4x+4=(x-2)2 | D. | x-1=x(1-$\frac{1}{x}$) |
18.如果多项式y2+my+16是完全平方式,那么m的值为( )
| A. | 8 | B. | -8 | C. | ±4 | D. | ±8 |
8.若xm+3x-6=0是关于x的一元二次方程,则m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.北国超市的小王对该超市苹果的销售进行了统计,某进价为2元/千克的品种的苹果每天的销售量y(千克)和当天的售价x(元/千克)之间满足y=-20x+200(3≤x≤5),若要使该品种苹果当天的利润达到最高,则其售价应为[利润=销售量•(售价-进价)]( )
| A. | 5元 | B. | 4元 | C. | 3.5元 | D. | 3元 |
12. 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
 如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则DB的长为( )| A. | $4\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
13.在△ABC中,∠ACB=90°,BC=1,AC=2,则下列正确的是( )
| A. | sinA=$\frac{2\sqrt{5}}{5}$ | B. | tanA=$\frac{\sqrt{5}}{5}$ | C. | cosB=$\frac{\sqrt{5}}{5}$ | D. | tanB=$\frac{1}{2}$ |
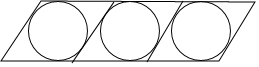 如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.
如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.