题目内容
5．化简（1-$\frac{2}{x+1}$）÷$\frac{1}{{x}^{2}-1}$的结果是（ ）| A． | （x+1）2 | B． | （x-1）2 | C． | $\frac{1}{（x+1）^{2}}$ | D． | $\frac{1}{（x-1）^{2}}$ |
分析 先对括号内的式子通分，然后再将除法转化为乘法即可解答本题．
解答 解：（1-$\frac{2}{x+1}$）÷$\frac{1}{{x}^{2}-1}$
=$\frac{x+1-2}{x+1}÷\frac{1}{（x+1）（x-1）}$
=$\frac{x-1}{x+1}•（x+1）（x-1）$
=（x-1）2，
故选B．
点评 本题考查分式的混合运算，解题的关键是明确分式的混合运算的计算方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．北国超市的小王对该超市苹果的销售进行了统计，某进价为2元/千克的品种的苹果每天的销售量y（千克）和当天的售价x（元/千克）之间满足y=-20x+200（3≤x≤5），若要使该品种苹果当天的利润达到最高，则其售价应为[利润=销售量•（售价-进价）]（ ）
| A． | 5元 | B． | 4元 | C． | 3.5元 | D． | 3元 |
16．在一次函数y=-x+2的图象上的点是（ ）
| A． | （-1，4） | B． | （2，0） | C． | （1，0） | D． | （2，1） |
13．在△ABC中，∠ACB=90°，BC=1，AC=2，则下列正确的是（ ）
| A． | sinA=$\frac{2\sqrt{5}}{5}$ | B． | tanA=$\frac{\sqrt{5}}{5}$ | C． | cosB=$\frac{\sqrt{5}}{5}$ | D． | tanB=$\frac{1}{2}$ |
20．已知直角三角形两直角边分别是3和4，将这两边扩大到原来的两倍，则斜边的长为（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
10．
如图，△ABC内接于⊙O，若∠OAB=26°，则∠C的大小为（ ）
如图，△ABC内接于⊙O，若∠OAB=26°，则∠C的大小为（ ）| A． | 26° | B． | 52° | C． | 60° | D． | 64° |
17．
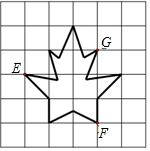如图所示，若点E的坐标为（-2，1），点F的坐标为（1，-1），则点G的坐标为（ ）
如图所示，若点E的坐标为（-2，1），点F的坐标为（1，-1），则点G的坐标为（ ）| A． | （1，2） | B． | （2，2） | C． | （2，1） | D． | （1，1） |
3．
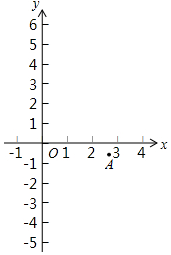有这样一个问题：探究函数y=（x-1）（x-2）（x-3）的图象与性质．小东对函数y=（x-1）（x-2）（x-3）的图象与性质进行了探究．
下面是小东的探究过程，请补充完成：
（1）函数y=（x-1）（x-2）（x-3）的自变量x的取值范围是全体实数；
（2）下表是y与x的几组对应值．
①m=-60；
②若M（-7，-720），N（n，720）为该函数图象上的两点，则n=11；
（3）在平面直角坐标系xOy中，A（xA，yA），B（xB，-yA）为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示．
①标出点B的位置；
②画出函数y=（x-1）（x-2）（x-3）（0≤x≤4）的图象．
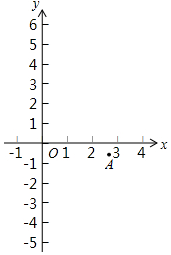有这样一个问题：探究函数y=（x-1）（x-2）（x-3）的图象与性质．小东对函数y=（x-1）（x-2）（x-3）的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）函数y=（x-1）（x-2）（x-3）的自变量x的取值范围是全体实数；
（2）下表是y与x的几组对应值．
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
②若M（-7，-720），N（n，720）为该函数图象上的两点，则n=11；
（3）在平面直角坐标系xOy中，A（xA，yA），B（xB，-yA）为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示．
①标出点B的位置；
②画出函数y=（x-1）（x-2）（x-3）（0≤x≤4）的图象．
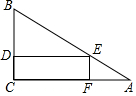一块三角形材料如图所示，∠A=30°，∠C=90°，AB=12，用这块材料剪出一个矩形CDEF，其中D、E、F分别在BC、AB、AC上．