题目内容
1.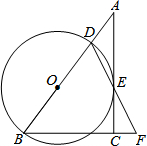 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长交BC的延长线于点F.(1)求证:∠BDF=∠F;
(2)如果CF=1,sinA=$\frac{3}{5}$,求⊙O的半径.
分析 (1)作辅助线,连接OE,根据切线的性质知OE⊥AC,已知∠ACB=90°,可知OE∥BC,得∠OED=∠F,再根据OD=OE,可知∠ODE=∠OED,从而可得∠BDE=∠F;
(2)根据sinA=$\frac{3}{5}$,得出cos∠B=cos∠AOE=$\frac{3}{5}$,进一步设出未知数,利用锐角三角函数的意义可将⊙O的半径求出.
解答 (1)证明:如图,连结OE.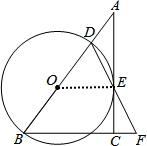
∵AC切⊙O于点E,
∴∠AEO=90°.
∵∠ACB=90°
∴∠ACB=∠AEO.
∴OE∥BC.
∴∠OED=∠BFD.
∵OE=OD,
∴∠OED=∠ODE.
∴∠BDF=∠F.
(2)解:∵OE∥BC,
∴∠AOE=∠B.
∵sin∠A=$\frac{3}{5}$,
∴cos∠B=cos∠AOE=$\frac{3}{5}$,
设OE=3x,则OA=5x,OB=3x.
∴BD=BF=6x,AB=8x.
∵CF=1,
∴BC=6x-1.
∵cos∠B=$\frac{BC}{AB}$=$\frac{6x-1}{8x}$=$\frac{3}{5}$.
解得x=$\frac{5}{6}$.
∴OB=3x=$\frac{5}{2}$.
∴⊙O的半径是$\frac{5}{2}$.
点评 本题考查了圆的切线性质,锐角三角函数的意义,结合几何图形,灵活作出辅助线解决问题.

练习册系列答案
相关题目
9.230 000用科学记数法表示应为( )
| A. | 0.23×105 | B. | 23×104 | C. | 2.3×105 | D. | 2.3×104 |
13.已知钝角三角形的三边为2、3、4,该三角形的面积为( )
| A. | $\frac{5\sqrt{13}}{4}$ | B. | $\frac{5\sqrt{15}}{4}$ | C. | $\frac{4\sqrt{13}}{5}$ | D. | $\frac{3\sqrt{15}}{4}$ |
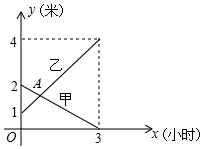 有甲、乙两个圆柱体的蓄水池,将甲池中的水以一定的速度注入乙池.甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,其中,甲蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式为y=-$\frac{2}{3}$x+2.结合图象回答:
有甲、乙两个圆柱体的蓄水池,将甲池中的水以一定的速度注入乙池.甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,其中,甲蓄水池中水的深度y(米)与注水时间x(时)之间的函数关系式为y=-$\frac{2}{3}$x+2.结合图象回答: