题目内容
13.已知钝角三角形的三边为2、3、4,该三角形的面积为( )| A. | $\frac{5\sqrt{13}}{4}$ | B. | $\frac{5\sqrt{15}}{4}$ | C. | $\frac{4\sqrt{13}}{5}$ | D. | $\frac{3\sqrt{15}}{4}$ |
分析 利用勾股定理得出BD的长,进而利用三角形面积求法得出答案.
解答 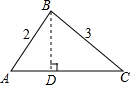 解:如图所示:过点B作BD⊥AC于点D,
解:如图所示:过点B作BD⊥AC于点D,
设BD=x,CD=y,
则AD=4-y,
故在Rt△BDC中,
x2+y2=32,
故在Rt△ABD中,
x2+(4-y)2=22,
故9+16-8y=4,
解得:y=$\frac{21}{8}$,
∴x2+($\frac{21}{8}$)2=9,
解得:x=$\frac{3\sqrt{15}}{8}$,
故三角形的面积为:$\frac{1}{2}$×4×$\frac{3\sqrt{15}}{8}$=$\frac{3\sqrt{15}}{4}$.
故选:D.
点评 此题主要考查了勾股定理,根据题意得出三角形的高的值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.据《梧州日报》报道,梧州黄埔化工药业有限公司位于万秀区松脂产业园,总投资119000000元,数字119000000用科学记数法表示为( )
| A. | 119×106 | B. | 11.9×107 | C. | 1.19×108 | D. | 0.119×109 |
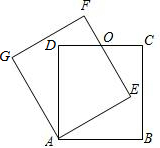 如图,正方形ABCD绕点A逆时针转n°后得到正方形AEFG,边EF与CD交于点O.若正方形边长为2cm,若旋转的角度为30°,求重叠部分四边形(AEOD)的面积.
如图,正方形ABCD绕点A逆时针转n°后得到正方形AEFG,边EF与CD交于点O.若正方形边长为2cm,若旋转的角度为30°,求重叠部分四边形(AEOD)的面积.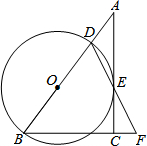 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长交BC的延长线于点F.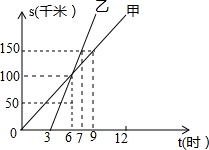 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.回答下列问题:
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.回答下列问题: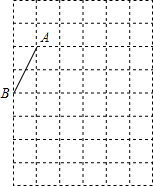 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.