题目内容
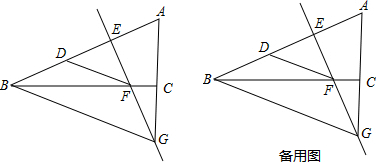
13.如图,在△ABC中,∠ACB=90°,点D为AB边上一点,AD的垂直平分线交AD于点E,交BC于点F,交AC的延长线于点G,连接DF,BG,∠EDF=45°.求证:(1)BF=AG;
(2)∠DFB=∠GBF.
分析 (1)首先证明∠ABC=∠AGE,然后结合题干条件利用AAS证明△EBF≌△EGA,于是得出结论;
(2)先根据全等三角形的性质得到BE=EG,进而得到∠EBG=∠EGB,于是得到∠EDF=∠EBG,利用平行线的知识得出结论.
解答 解:(1)∵EF是AD的垂直平分线,
∴∠DEF=∠AEF=90°,DE=AE,
∵∠EDF=45°,
∴∠EDF=∠DFE=45°,
∴DE=EF,
∵DE=AE,
∴AE=EF,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠A+∠AGE=90°,
∴∠ABC=∠AGE,
在△AEG和△FEB中,
∵$\left\{\begin{array}{l}{∠EBF=∠EGA}\\{∠BEF=∠GEA}\\{EF=AE}\end{array}\right.$,
∴△EBF≌△EGA,
∴BF=AG;
(2)由(1)知△EBF≌△EGA,
∴BE=EG,
∴∠EBG=∠EGB,
∵∠BEG=90°,
∴∠EBG=∠EGB=45°,
∵∠EDF=45°,
∴∠EDF=∠EBG,
∴DF∥BG,
∴∠DFB=∠GBF.
点评 本题主要考查了全等三角形的判定与性质,解(1)问的关键是利用AAS证明△EBF≌△EGA,解(2)问的关键是证明出∠EDF=∠EBG,此题难度一般.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
3.微山湖自古就有“日出斗金”之美誉,助推着周边地区经济的发展,某公司加工生产了A、B、C三类湖产品,销售的重量及利润如表所示:
该公司计划用26辆汽车装载三类湖产品(毎类湖产品至少一辆车,每辆汽车只装一类湖产品且装满)共48吨到某地销售.
(1)设装A类湖产品用x辆汽车,装B类湖产品用y辆汽车,装C类湖产品用z辆汽车.请用含z的式子表示x,y.
(2)如果本次销售公司获得利润为w万元,那么如何安排装运,可使w最大,最大是多少万元?
| 湖产品种类 | A类 | B类 | C类 |
| 每辆汽车装载吨数 | 2 | 1 | 1.5 |
| 每吨湖产品可获利润(万元) | 5 | 7 | 4 |
(1)设装A类湖产品用x辆汽车,装B类湖产品用y辆汽车,装C类湖产品用z辆汽车.请用含z的式子表示x,y.
(2)如果本次销售公司获得利润为w万元,那么如何安排装运,可使w最大,最大是多少万元?
 如图,l1∥l2∥l3,且l1和l2间的距离是5,l2和l3间的距离是7,若正方形有三个顶点分别在三条直线上,则此正方形的面积最小是74.
如图,l1∥l2∥l3,且l1和l2间的距离是5,l2和l3间的距离是7,若正方形有三个顶点分别在三条直线上,则此正方形的面积最小是74. 如图,直线l与直线a,b,c分别交于点A,B,C,a∥b,l⊥a,l⊥c,AB=2.
如图,直线l与直线a,b,c分别交于点A,B,C,a∥b,l⊥a,l⊥c,AB=2. 如图,已知△ABC.
如图,已知△ABC. 如图,把矩形ABCD纸片沿着过点A的直线AE折叠,使得点D落在BC边上的点F处,若∠BAF=40°,则∠DAE=25°.
如图,把矩形ABCD纸片沿着过点A的直线AE折叠,使得点D落在BC边上的点F处,若∠BAF=40°,则∠DAE=25°.