题目内容
1. 如图,直线l与直线a,b,c分别交于点A,B,C,a∥b,l⊥a,l⊥c,AB=2.
如图,直线l与直线a,b,c分别交于点A,B,C,a∥b,l⊥a,l⊥c,AB=2.(1)填空:l与b的位置关系是l⊥b,c与b的位置关系是c∥b;
(2)已知M是直线a上点,N是直线c上点,D是直线b上点,且S△BDM=$\frac{2}{3}$S△BOM,求a,c间的距离.
分析 (1)根据a∥b,l⊥a,得到l⊥b,l与b的位置关系是:l⊥b,根据l⊥b,l⊥c,得到c与b的位置关系是:c∥b,
(2)根据三角形BDM的BD边上的高为点M到直线b的距离,得到AB=2; 由三角形BDN的BD边上的高为点N到直线b的距离,得到BC; 根据三角形的面积公式列方程即可得到结论.
解答 解:(1)∵a∥b,l⊥a,
∴l⊥b,l与b的位置关系是:l⊥b,
∵l⊥b,l⊥c,
∴c与b的位置关系是:c∥b,
故答案为:l⊥b,c∥b;
(2)因为三角形BDM的BD边上的高为点M到直线b的距离,即为AB=2;
三角形BDN的BD边上的高为点N到直线b的距离,即为BC;
由S△BDM=$\frac{2}{3}$S△BDN,
得$\frac{1}{2}$×BD•AB=$\frac{2}{3}$×$\frac{1}{2}$BD•BC,
故BC=3,
所以a,c间的距离为5.
点评 本题考查了平行线的判定和性质,平行线之间的距离,三角形的面积,熟练掌握平行线的判定和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,PF∥BC交AB于F,连接PQ交AB于D.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,PF∥BC交AB于F,连接PQ交AB于D. 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,BD与AE交于点F.
 如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD,垂足为F,交BC的延长线于点E,BE=a,CE=c,DE=b,求证:关于x的一元二次方程x2-2bx+ac=0有两个相等的实根.
如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD,垂足为F,交BC的延长线于点E,BE=a,CE=c,DE=b,求证:关于x的一元二次方程x2-2bx+ac=0有两个相等的实根.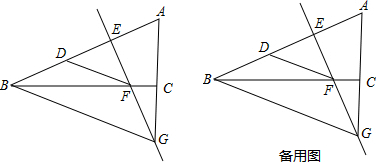
 如图,Rt△ABC中,D为斜边AB的中点,AB=7,延长AC到E使得CE=CA,连结BE,则线段BE的长为7.
如图,Rt△ABC中,D为斜边AB的中点,AB=7,延长AC到E使得CE=CA,连结BE,则线段BE的长为7.