题目内容
18. 如图,已知△ABC.
如图,已知△ABC.(1)若AB=4,AC=5,则BC边的取值范围是1<BC<9;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
分析 (1)利用三角形的三边关系确定第三边的取值范围即可;
(2)首先利用平行线的性质确定∠EDB的度数,然后利用三角形内角和定理确定∠B的度数即可.
解答 解:(1)∵AB=4,AC=5,
∴5-4<BC<4+5,
即1<BC<9,
故答案为:1<BC<9;
(2)∵∠ACD=125°,
∴∠ACB=180°-∠ACD=55°,
∵DE∥AC,
∴∠BDE=∠ACB=55°.
∵∠E=55°,
∴∠B=180°-∠E-∠BDE=180°-55°-55°=70°.
点评 本题考查了三角形的三边关系及平行线的性质,解题的关键是能够了解三角形的三边关系及两直线平行同位角相等的知识,难度不大.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
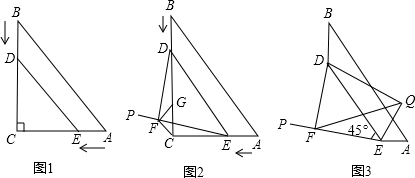

 如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD,垂足为F,交BC的延长线于点E,BE=a,CE=c,DE=b,求证:关于x的一元二次方程x2-2bx+ac=0有两个相等的实根.
如图,在△ABC中,AD是∠BAC的平分线,EF垂直平分AD,垂足为F,交BC的延长线于点E,BE=a,CE=c,DE=b,求证:关于x的一元二次方程x2-2bx+ac=0有两个相等的实根.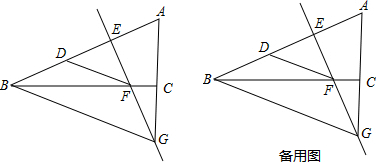
 如图,点O是AC的中点,BO=OD,∠ABC和∠DAB互为补角吗?为什么?
如图,点O是AC的中点,BO=OD,∠ABC和∠DAB互为补角吗?为什么? 如图,Rt△ABC中,D为斜边AB的中点,AB=7,延长AC到E使得CE=CA,连结BE,则线段BE的长为7.
如图,Rt△ABC中,D为斜边AB的中点,AB=7,延长AC到E使得CE=CA,连结BE,则线段BE的长为7. 如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,判断AC与BD的位置关系,并说明理由.
如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,判断AC与BD的位置关系,并说明理由.