题目内容
12.某校学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的办法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成右边的两幅不完整的统计图(如图1,图2,要求每位同学只能选择一种自己喜欢的球类;图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数),请你根据图中提供的信息,解答下列问题:(1)在这次研究中,一共调查了多少名学生?
(2)喜欢排球的人数在扇形统计图中所占的圆心角是多少度?
(3)补全频数分布折线统计图.

分析 (1)根据爱好乒乓球的人数有20和所占的百分比为20%,可以求得在这次研究中,一共调查了多少名学生;
(2)根据爱好的排球的人数占调查人数的百分比,再乘以360°,可以求得喜欢排球的人数在扇形统计图中所占的圆心角;
(3)根据题目中的信息可以求得爱好篮球和排球的人数,从而可以将折线统计图补充完整.
解答  解:(1)20÷20%=100,
解:(1)20÷20%=100,
即在这次研究中,一共调查了100名学生;
(2)喜欢排球的人数在扇形统计图中所占的圆心角是:360°×(1-20%-40%-$\frac{30}{100}$)=36°,
即喜欢排球的人数在扇形统计图中所占的圆心角是36°;
(3)喜欢篮球的学生有:100×40%=40(人),
喜欢排球的学生有:100-30-20-40=10(人),
故补全的频数分布折线统计图如右图所示,
点评 本题考查频数(率)分布折线图、扇形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
相关题目
1.已知,不等式组$\left\{\begin{array}{l}{x>a}\\{-x+5>0}\end{array}\right.$只有3个整数解,则a的取值范围是( )
| A. | 1<x<2 | B. | 1≤x<2 | C. | 1<x≤2 | D. | 1≤x≤2 |
2.下列命题中真命题的是( )
| A. | 如果a=b,b=c,那么a=c | B. | 如果a<0,b<0,那么ab<0 | ||
| C. | 内错角相等 | D. | 一个角的补角大于这个角 |
19.顺次连接一个矩形各边的中点,得到的四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
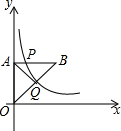 如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,
如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,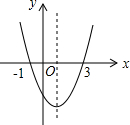 图为二次函数y=ax2+bx+c的图象,给出下列说法:
图为二次函数y=ax2+bx+c的图象,给出下列说法: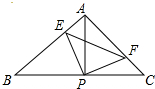 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( ) 请将下列证明过程补充完整:
请将下列证明过程补充完整: