题目内容
2. 请将下列证明过程补充完整:
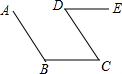
请将下列证明过程补充完整:已知:如图,AB∥DC,BC∥DE.
求证:∠B+∠D=180°.
证明:∵BC∥DE(已知)
∴∠C=∠D(两直线平行,内错角相等).
∵AB∥DC(已知)
∴∠B+∠C=180°(两直线平行,同旁内角互补).
∴∠B+∠D=180°(等量代换).
分析 根据平行线的性质得到∠C=∠D,∠B+∠C=180°,等量代换即可得到结论.
解答 证明:∵BC∥DE(已知)
∴∠C=∠D(两直线平行,内错角相等).
∵AB∥DC,(已知)
∴∠B+∠C=180°(两直线平行,同旁内角互补).
∴∠B+∠D=180°(等量代换).
故答案为:已知,∠D,两直线平行,内错角相等,AB∥DC,两直线平行,同旁内角互补,等量代换.
点评 此题主要考查平行线的性质:两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
11.下列各组线段中,能构成直角三角形的一组是( )
| A. | 7,12,13 | B. | 5,9,12 | C. | 3,4,6 | D. | 40,50,30 |
12.下列等式中,正确的是( )
| A. | 3a-2a=1 | B. | (a2)3=a5 | C. | (-2a3)2=4a6 | D. | (a-b)2=a2-b2 |

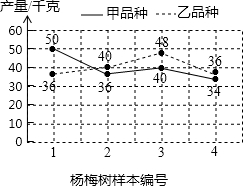 果树改良实验基地育有甲、乙两个品种的杨梅树各100棵,到了收获季,为了分析收成情况,分别从两个品种中随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
果树改良实验基地育有甲、乙两个品种的杨梅树各100棵,到了收获季,为了分析收成情况,分别从两个品种中随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. 如图,数轴上表示的是关于x的不等式组中两个不等式的解集,则这个不等式组的解集为2≤x≤3.
如图,数轴上表示的是关于x的不等式组中两个不等式的解集,则这个不等式组的解集为2≤x≤3.