题目内容
10. 市政广场前有块形状为直角三角形的绿地(如图所示),其中AC=8m,BC=6m.为广场整体布局考虑,现在将原绿地扩充成等腰三角形,且扩充所增加的部分要求是以AC为直角边的直角三角形.请求出扩充建设后所得等腰三角形绿地的周长.
市政广场前有块形状为直角三角形的绿地(如图所示),其中AC=8m,BC=6m.为广场整体布局考虑,现在将原绿地扩充成等腰三角形,且扩充所增加的部分要求是以AC为直角边的直角三角形.请求出扩充建设后所得等腰三角形绿地的周长.
分析 根据题意画出图形,分AB=AD,AB=BD,AD=BD三种情况进行讨论即可.
解答 解:在Rt△ABC中,∠ACB=90°,AC=8,BC=6,
根据勾股定理得:$\sqrt{A{C}^{2}+B{C}^{2}}$=10本题可分为三种情况,讨论如下:
(1)如图1,当AB=AD=10时,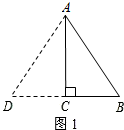
在Rt△ABC中,根据勾股定理得:
CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=6,
∴△ABD的周长=10+10+6×2=32m;
(2)如图2,当AB=BD=10时,
∵BC=6,
∴CD=BD-BC=10-6=4,
在Rt△ACD中,根据勾股定理得:
∴△ABD的周长=10+10+4$\sqrt{5}$=(20+4$\sqrt{5}$)m,
(3)如图3,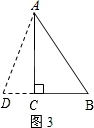
当AB为底,AD=BD时,设AD=BD=x,则CD=x-6,
在Rt△ACD中,根据勾股定理得:
AC2+CD2=AD2,
即82+(x-6)2=x2,
解得:x=$\frac{25}{3}$,
∴△ABD的周长=10+$\frac{25}{3}$×2=$\frac{80}{3}$m,
∴扩充后的绿地的周长为:32m或(20+4$\sqrt{5}$)m或$\frac{80}{3}$m.
点评 本题考查的是勾股定理的应用,熟知在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用是解答此题的关键.

练习册系列答案
相关题目
18.某蔬菜经营户,用160元从某蔬菜市场批发了茄子和豆角共50千克,茄子、豆角当天的批发价和零售价如下表所示:
(1)这天该经营户批发了茄子和豆角各多少千克?
(2)当天卖完这些茄子和豆角共可盈利多少元?
| 品名 | 茄子 | 豆角 |
| 批发价(元/千克) | 3.0 | 3.5 |
| 零售价(元/千克) | 4.5 | 5.2 |
(2)当天卖完这些茄子和豆角共可盈利多少元?
8.若分式$\frac{|x|-3}{{x}^{2}-9}$的值为零,则x的值为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 不存在 |
 如图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于30°.
如图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于30°.
 如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是4$\sqrt{3}$.
如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是4$\sqrt{3}$.