题目内容
5.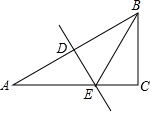 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
分析 由ED是线段AB的垂直平分线,根据线段垂直平分线定理得到EA=EB,根据等边对等角可得∠A和∠ABE相等,由∠A的度数求出∠ABE的度数,得出∠EBC=∠EBA=30°,再由角平分线上的点到角的两边的距离相等得出DE=CE=2.由30°角所对的直角边等于斜边的一半,可得AE=2ED=4,由勾股定理求出AD,那么AB=2AD.
解答  解:∵在Rt△ABC中,∠C=90°,∠ABC=60°,
解:∵在Rt△ABC中,∠C=90°,∠ABC=60°,
∴∠A=30°,
∵DE是线段AB的垂直平分线,
∴EA=EB,ED⊥AB,
∴∠A=∠EBA=30°,
∴∠EBC=∠ABC-∠EBA=30°,
又∵BC⊥AC,ED⊥AB,
∴DE=CE=2.
在直角三角形ADE中,DE=2,∠A=30°,
∴AE=2DE=4,
∴AD=$\sqrt{A{E}^{2}-D{E}^{2}}$=2$\sqrt{3}$,
∴AB=2AD=4$\sqrt{3}$.
故选B.
点评 此题考查了线段垂直平分线的性质,角平分线的性质,含30°角的直角三角形的性质,勾股定理,解题的关键是熟练掌握含30°角的直角三角形的性质,即在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
15. 如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=35°,则∠C的度数为( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
16.当x=3时,分式($\frac{x^2}{x-1}$-x-1)÷$\frac{x}{{{x^2}-1}}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
20. 某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
 某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )
某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}x>4\\ x≤-1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<4\\ x≥-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>4\\ x>-1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x≤4\\ x>-1\end{array}\right.$ |
10.已知$\frac{x}{y}$=$\frac{3}{4}$,那么下列各式中正确的是( )
| A. | $\frac{y}{x+y}$=$\frac{4}{7}$ | B. | $\frac{x}{x-y}$=3 | C. | $\frac{x+2y}{x}$=$\frac{10}{3}$ | D. | $\frac{x-y}{y}$=$\frac{1}{4}$ |
17.下列四个几何体中,主视图与俯视图相同的是( )
| A. |  | B. |  | C. |  | D. |  |




