题目内容
15．
如图，AD是∠EAC的平分线，AD∥BC，∠B=35°，则∠C的度数为（ ）| A． | 55° | B． | 45° | C． | 35° | D． | 25° |
分析 由AD∥BC，∠B=35°利用平行线的性质即可得出∠EAD的度数，再根据角平分线的定义即可求出∠EAC的度数，最后由三角形的外角的性质即可得出∠EAC=∠B+∠C，代入数据即可得出结论．
解答 解：∵AD∥BC，∠B=35°，
∴∠EAD=∠B=35°．
又∵AD是∠EAC的平分线，
∴∠EAC=2∠EAD=70°．
∵∠EAC=∠B+∠C，
∴∠C=∠EAC-∠B=35°．
故选C．
点评 本题考查了平行线的性质、三角形外角性质以及角平分线的定义，解题的关键是求出∠EAC=60°．解决该题型题目时，根据平行线的性质找出相等或互补的角是关键．
练习册系列答案
相关题目
5．
如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：
①a-b+c＞0；
②3a+b=0；
③b2=4a（c-n）；
④一元二次方程ax2+bx+c=n-1有两个互异实根．
其中正确结论的个数是（ ）
如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＞0；
②3a+b=0；
③b2=4a（c-n）；
④一元二次方程ax2+bx+c=n-1有两个互异实根．
其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
6．
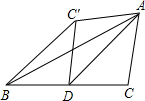如图，AD为△ABC的BC边上的中线，沿AD将△ACD折叠，C的对应点为C′，已知∠ADC=45°，BC=6，那么点B与C′的距离为（ ）
如图，AD为△ABC的BC边上的中线，沿AD将△ACD折叠，C的对应点为C′，已知∠ADC=45°，BC=6，那么点B与C′的距离为（ ）| A． | 3 | B． | 3$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 6 |
用五块大小相同的小正方体搭成如图所示的几何体，这个几何体的俯视图是（ ）
10．图是一组有规律的图案，它们是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，依此规律，第n个图案中涂有阴影的小正方形个数为（ ）
| A． | 5n | B． | （5n-1） | C． | （5n-2） | D． | （4n+1） |
20．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
4．下列运算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | a8÷a4=a2 | C． | 2a+3b=5ab | D． | a2•a3=a5 |
5．
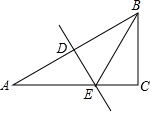如图，在Rt△ABC中，∠C=90°，∠ABC=60°，AB的垂直平分线分别交AB与AC于点D和点E．若CE=2，则AB的长是（ ）
如图，在Rt△ABC中，∠C=90°，∠ABC=60°，AB的垂直平分线分别交AB与AC于点D和点E．若CE=2，则AB的长是（ ）| A． | 4 | B． | 4$\sqrt{3}$ | C． | 8 | D． | 8$\sqrt{3}$ |