题目内容
16.当x=3时,分式($\frac{x^2}{x-1}$-x-1)÷$\frac{x}{{{x^2}-1}}$的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
分析 先化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:($\frac{x^2}{x-1}$-x-1)÷$\frac{x}{{{x^2}-1}}$
=$\frac{{x}^{2}-(x+1)(x-1)}{x-1}•\frac{(x+1)(x-1)}{x}$
=$\frac{1}{x-1}•\frac{(x+1)(x-1)}{x}$
=$\frac{x+1}{x}$,
当x=3时,原式=$\frac{3+1}{3}=\frac{4}{3}$,
故选B.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的计算方法.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.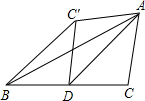 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |
4.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | a8÷a4=a2 | C. | 2a+3b=5ab | D. | a2•a3=a5 |
11.不等式组$\left\{\begin{array}{l}{2x+1≤3}\\{x+3>4}\end{array}\right.$的解集是( )
| A. | x>1 | B. | x≤1 | C. | x=1 | D. | 无解 |
1.若二次根式$\sqrt{3x-2}$有意义,则x的取值范围是( )
| A. | x≥$\frac{2}{3}$ | B. | x≤$\frac{2}{3}$ | C. | x≥$\frac{3}{2}$ | D. | x≤$\frac{3}{2}$ |
8. 如图,已知AD∥BC,∠B=32°,DB平分∠ADE,则∠DEC=( )
如图,已知AD∥BC,∠B=32°,DB平分∠ADE,则∠DEC=( )
 如图,已知AD∥BC,∠B=32°,DB平分∠ADE,则∠DEC=( )
如图,已知AD∥BC,∠B=32°,DB平分∠ADE,则∠DEC=( )| A. | 64° | B. | 66° | C. | 74° | D. | 86° |
5.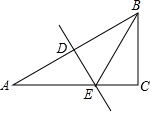 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )
 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB与AC于点D和点E.若CE=2,则AB的长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
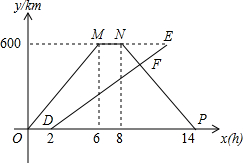 A、B两地相距600km,甲、乙两车都从A地出发,沿着同一路线匀速驶向B地,乙车比甲车晚出发2h,甲车到达B地停留2h立即按原路匀速返回,图中折线OMNP和线段DE分别是两车离A地的距离y(km)与甲车行驶时间x(h)之间的函数图象.
A、B两地相距600km,甲、乙两车都从A地出发,沿着同一路线匀速驶向B地,乙车比甲车晚出发2h,甲车到达B地停留2h立即按原路匀速返回,图中折线OMNP和线段DE分别是两车离A地的距离y(km)与甲车行驶时间x(h)之间的函数图象.