题目内容
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“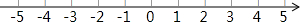 数形结合”的基础.
数形结合”的基础.
(1)在数轴上标示出-4、-3、-2、4;
(2)结合数轴与绝对值的知识回答下列问题:
①数轴上表示4和-2的两点之间的距离是 ,
表示-2和-4两点之间的距离是 ;
一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.如果表示数a和-2的两点之间的距离是3,即|a-(-2)|=3,那么a= ;
②若数轴上表示数a的点位于-3和2之间,则|a+3|+|a-2|的值是 ;
③当a取 时,|a+5|+|a-1|+|a-4|的值最小,最小值是 .
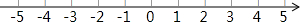 数形结合”的基础.
数形结合”的基础.(1)在数轴上标示出-4、-3、-2、4;
(2)结合数轴与绝对值的知识回答下列问题:
①数轴上表示4和-2的两点之间的距离是
表示-2和-4两点之间的距离是
一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.如果表示数a和-2的两点之间的距离是3,即|a-(-2)|=3,那么a=
②若数轴上表示数a的点位于-3和2之间,则|a+3|+|a-2|的值是
③当a取
考点:数轴
专题:
分析:(1)在数轴上标示出-4、-3、-2、4即可求解;
(2)①根据两点间的距离是大数减小数,可得答案;
②根据|a+3|+|a-2|表示数a的点到-3与2两点的距离的和.即可求解;
③根据|a+5|+|a-1|+|a-4|表示一点到-5,1,4三点的距离的和.即可求解.
(2)①根据两点间的距离是大数减小数,可得答案;
②根据|a+3|+|a-2|表示数a的点到-3与2两点的距离的和.即可求解;
③根据|a+5|+|a-1|+|a-4|表示一点到-5,1,4三点的距离的和.即可求解.
解答:解:(1)如图所示:

(2)①数轴上表示4和-2的两点之间的距离是4-(-2)=6,
表示-2和-4两点之间的距离是-2-(-4)=2;
∵|a-(-2)|=3,
∴a-(-2)=±3,
解得a=-5或1;
②因为|a+3|+|a-2|表示数轴上数a和-4,2之间距离的和.
又因为数a位于-3与2之间,
所以|a+3|+|a-2|=5;
③根据|a+5|+|a-1|+|a-4|表示一点到-5,1,4三点的距离的和.
所以当a=1时,式子的值最小,
此时|a+5|+|a-1|+|a-4|的最小值是9.
故答案为:6,2,-5或1;5;1,9.

(2)①数轴上表示4和-2的两点之间的距离是4-(-2)=6,
表示-2和-4两点之间的距离是-2-(-4)=2;
∵|a-(-2)|=3,
∴a-(-2)=±3,
解得a=-5或1;
②因为|a+3|+|a-2|表示数轴上数a和-4,2之间距离的和.
又因为数a位于-3与2之间,
所以|a+3|+|a-2|=5;
③根据|a+5|+|a-1|+|a-4|表示一点到-5,1,4三点的距离的和.
所以当a=1时,式子的值最小,
此时|a+5|+|a-1|+|a-4|的最小值是9.
故答案为:6,2,-5或1;5;1,9.
点评:本题主要考查了数轴,绝对值的定义,就是表示两点之间的距离.

练习册系列答案
相关题目
若|a|=1,b2=4,且ab<0,则a-b的值是( )
| A、-3或3 | B、-1或3 |
| C、3 | D、-3 |
 如图,△ABC中,∠C=45°,若MP和NQ分别垂直平分AB和AC,CQ=4,PQ=3,求BC的长.
如图,△ABC中,∠C=45°,若MP和NQ分别垂直平分AB和AC,CQ=4,PQ=3,求BC的长.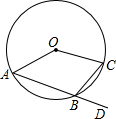 如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=
如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC= 如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.