题目内容
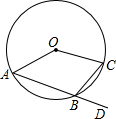 如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=
如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=考点:圆内接四边形的性质,圆周角定理
专题:
分析:设点E是优弧AB(不与A,B重合)上的一点,则∠AEC=
∠AOC,根据圆内接四边形的外角等于它的内对角即可求得.
| 1 |
| 2 |
解答: 解:设点E是优弧AB(不与A,B重合)上的一点,连接AE、CE,
解:设点E是优弧AB(不与A,B重合)上的一点,连接AE、CE,
∵∠CBD=65°.
∴∠E=180°-∠CBD=65°.
∴∠AOC=2∠E=130°.
故答案是:130.
 解:设点E是优弧AB(不与A,B重合)上的一点,连接AE、CE,
解:设点E是优弧AB(不与A,B重合)上的一点,连接AE、CE,∵∠CBD=65°.
∴∠E=180°-∠CBD=65°.
∴∠AOC=2∠E=130°.
故答案是:130.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.和圆内接四边形对角互补的知识.

练习册系列答案
相关题目
有一种记分方法:以80为准,88分记为+8分,某同学得分为73分,则应记为( )
| A、+73分 | B、-73分 |
| C、+7分 | D、-7分 |
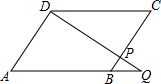 如图,已知点P是?ABCD的边BC上的一点,连接OP并延长交AB的延长线于点Q,
如图,已知点P是?ABCD的边BC上的一点,连接OP并延长交AB的延长线于点Q, 数形结合”的基础.
数形结合”的基础.