题目内容
 如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
如图,在直角坐标系xOy中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标.
考点:待定系数法求二次函数解析式,三角形的面积
专题:
分析:(1)直接把原点坐标代入y=x2+(2k-1)x+k+1求出k的值即可得到二次函数解析式;
(2)先确定A(3,0)和抛物线的对称轴,设B(x,x2-3x),再根据三角形面积公式得到
•3•|x2-3x|=6,则x2-3x=4或x2-3x=-4,然后分别解方程求出x即可确定满足条件的B点坐标.
(2)先确定A(3,0)和抛物线的对称轴,设B(x,x2-3x),再根据三角形面积公式得到
| 1 |
| 2 |
解答:解:(1)把(0,0)代入得k+1=0,解得k=-1,
所以二次函数解析式为y=x2-3x;
(2)当y=0时,x2-3x=0,解得x1=0,x2=3,则A(3,0),
抛物线的对称轴为直线x=
,
设B(x,x2-3x),
因为△AOB的面积等于6,
所以
•3•|x2-3x|=6,
当x2-3x=4时,解得x1=-1,x2=4,则B点坐标为(4,4);
当x2-3x=-4时,方程无实数解.
所以点B的坐标为(4,4).
所以二次函数解析式为y=x2-3x;
(2)当y=0时,x2-3x=0,解得x1=0,x2=3,则A(3,0),
抛物线的对称轴为直线x=
| 3 |
| 2 |
设B(x,x2-3x),
因为△AOB的面积等于6,
所以
| 1 |
| 2 |
当x2-3x=4时,解得x1=-1,x2=4,则B点坐标为(4,4);
当x2-3x=-4时,方程无实数解.
所以点B的坐标为(4,4).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
有一种记分方法:以80为准,88分记为+8分,某同学得分为73分,则应记为( )
| A、+73分 | B、-73分 |
| C、+7分 | D、-7分 |
 数形结合”的基础.
数形结合”的基础.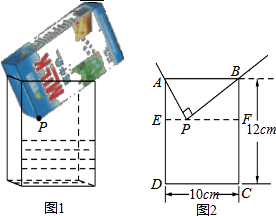 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.