题目内容
10.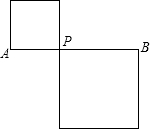 如图,AB=n,P是线段AB上一点,分别以AP、BP为边作正方形.
如图,AB=n,P是线段AB上一点,分别以AP、BP为边作正方形.(1)设AP=x,求两个正方形的面积之和S(用含有n、x的代数式表示);
(2)当AP分别为$\frac{1}{2}$n和$\frac{1}{3}$n时,比较S的大小.
分析 (1)表示出两正方形的边长,即可表示出两个正方形面积之和;
(2)把AP代入计算确定出S,比较即可.
解答 解:(1)S=x2+(n-x)2=2x2-2nx+n2;
(2)当AP=$\frac{1}{3}n$时,S=$\frac{5}{9}$n2,
当AP=$\frac{1}{2}n$时,S=$\frac{1}{2}$n2,
由$\frac{5}{9}$n2>$\frac{1}{2}$n2,得当AP=$\frac{1}{3}n$时,面积S较小.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知n是正整数,且$\sqrt{45n}$也是一个正整数,则正整数n的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
20.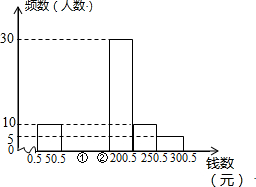 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
| 分 组 | 频数 | 所占比例 |
| 0.5~50.5 | 10 | 0.1 |
| 50.5~100.5 | 20 | 0.2 |
| 100.5~150.5 | 35 | 35 |
| 150.5~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
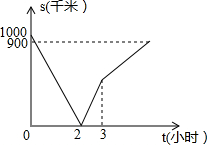 甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示
甲、乙、丙三地在一条直线上,乙地在甲地和丙地之间,一列高速列车从甲地开往乙地,一列快速列车从丙地经乙地开往甲地,两列列车同时出发,匀速行驶,且到达各自目的地后停止运行,从两列列车出发开始,至快速列车到达甲地为止,两列列车的距离s(千米)与行驶时间t(小时)之间的函数图象如图所示 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.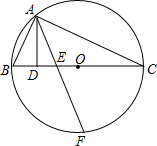 如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,
如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,