题目内容
6．已知代数式A=x2+xy+2y-$\frac{1}{2}$，B=2x2-2xy+x-1（1）求2A-B；
（2）当x=-1，y=-2时，求2A-B的值；
（3）若2A-B的值与x的取值无关，求y的值．
分析 （1）把A与B代入2A-B中，去括号合并即可得到结果；
（2）把x与y的值代入2A-B计算即可得到结果；
（3）由2A-B与x取值无关，确定出y的值即可．
解答 解：（1）2A-B=2（x2+xy+2y-$\frac{1}{2}$）-（2x2-2xy+x-1）=4xy+4y-x；
（2）当x=-1，y=-2时，2A-B=4xy+4y-x=4×（-1）×（-2）+4×（-2）-（-1）=1；
（3）由（1）可知2A-B=4xy+4y-x=（4y-1）x+4y
若2A-B的值与x的取值无关，则4y-1=0，
解得：y=-$\frac{1}{4}$．
点评 此题考查了有理数的减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17．
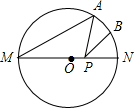如图，MN是半径为2的⊙O的直径，点A在⊙O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为（ ）
如图，MN是半径为2的⊙O的直径，点A在⊙O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB的最小值为（ ）| A． | 4$\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
11．3的相反数是（ ）
| A． | -3 | B． | 3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
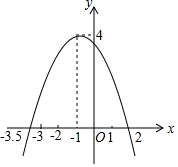如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点（2，0）和（-3.5，0），顶点为（-1，4），根据图象直接写出下列答案．