题目内容
17.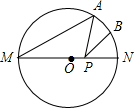 如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )| A. | 4$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 首先利用在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点P的位置,然后根据弧的度数发现一个等腰直角三角形计算.
解答 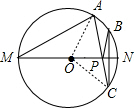 解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
解:作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数是60°,
则弧BN的度数是30°,
根据垂径定理得弧CN的度数是30°,
则∠AOC=90°,又OA=OC=2,
则AC=2$\sqrt{2}$.
故选C.
点评 此题主要考查了轴对称-最短路线问题,垂径定理,直角三角形的性质等,确定点P的位置是本题的关键.

练习册系列答案
相关题目
2.如图,观察图形并解答问题.

(1)按如表已填写的形式填写表中的空格,答案写在相应的序号后面:
(2)请用你发现的规律求出图④中的数x.

(1)按如表已填写的形式填写表中的空格,答案写在相应的序号后面:
| 图① | 图② | 图③ | |
| 三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | ② |
| 三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | ③ |
| 积与和的商 | (-2)÷2=-1 | ① | ④ |
9.现给出以下几个命题:
(1)长度相等的两条弧是等弧;
(2)相等的弧所对的弦相等;
(3)平分于弦的直径垂直这条弦并且平分弦所对的两条弧;
(4)钝角三角形的外接圆圆心在三角形外面;
(5)矩形的四个顶点必在同一个圆上;
其中真命题的个数有( )
(1)长度相等的两条弧是等弧;
(2)相等的弧所对的弦相等;
(3)平分于弦的直径垂直这条弦并且平分弦所对的两条弧;
(4)钝角三角形的外接圆圆心在三角形外面;
(5)矩形的四个顶点必在同一个圆上;
其中真命题的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.已知代数式A=x2+xy+2y-$\frac{1}{2}$,B=2x2-2xy+x-1
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
7.已知点(-3,y1),(1,y2)都在直线y=-$\frac{1}{2}$x+2上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
 如图实数在数轴上表示为:化简:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.
如图实数在数轴上表示为:化简:$\sqrt{{a}^{2}}$-|a-b|-|c-a|+$\sqrt{(b-c)^{2}}$.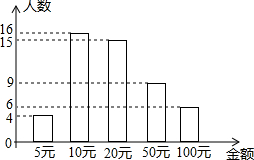 如图所示是某班50名学生的捐款情况统计图,根据图中信息可得捐款金额的中位数是20元.
如图所示是某班50名学生的捐款情况统计图,根据图中信息可得捐款金额的中位数是20元. 如图,AB∥CD,若∠1=30°,则∠2的度数为150°.
如图,AB∥CD,若∠1=30°,则∠2的度数为150°.