题目内容
15.若点P1(1,-3),P2(m,3)在同一反比例函数的图象上,则m的值为-1.分析 设反比例函数解析式为y=$\frac{k}{x}$,根据题意可得k=1×(-3)=-3,k=3m,进而可得3m=-3,再解即可.
解答 解:设反比例函数解析式为y=$\frac{k}{x}$,
∵点P1(1,-3),P2(m,3)在同一反比例函数的图象上,
∴k=1×(-3)=-3,k=3m,
∴3m=-3,
m=-1,
故答案为:-1.
点评 此题主要考查了反比例函数图象上点的坐标特点,关键是掌握图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
6.已知代数式A=x2+xy+2y-$\frac{1}{2}$,B=2x2-2xy+x-1
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
7.已知点(-3,y1),(1,y2)都在直线y=-$\frac{1}{2}$x+2上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
 如图,AB∥CD,若∠1=30°,则∠2的度数为150°.
如图,AB∥CD,若∠1=30°,则∠2的度数为150°.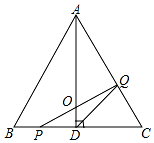 如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,当一个到达终点时,另一个也停止运动.设它们运动的时间为x(s).
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,当一个到达终点时,另一个也停止运动.设它们运动的时间为x(s).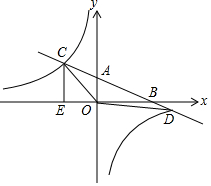 直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2.
直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2. 如图,在△ABC中,点D是BC的中点,点G为△ABC的重心,AG=2,则DG=1.
如图,在△ABC中,点D是BC的中点,点G为△ABC的重心,AG=2,则DG=1. 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则△OBD≌△OAC的判定方法是SAS(用字母表示)