题目内容
7.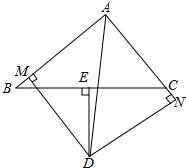 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
分析 连DB、DC,根据角平分线性质得DM=DN;根据垂直平分线的性质得DB=DC;再根据“HL”定理证明Rt△EFB≌Rt△EGC,从而得BM=CN.
解答 证明:连接DB、DN.
∵AD是∠BAC的平分线,
且DM⊥AB于M,DN⊥AC于N,
∴DM=DN.
∵DE⊥BC于E,E是BC的中点,
∴DB=DC.
在RT△DMB和RT△DNC中,
$\left\{\begin{array}{l}{DM=DN}\\{DB=DC}\end{array}\right.$
∴Rt△EFB≌Rt△EGC,
∴BM=CN.
点评 本题考查了角平分线性质和垂直平分线的性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键,属于中考常考题型.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
1.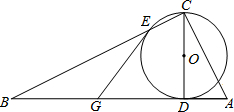 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
(1)求证:GE为⊙O的切线;
(2)若tanB=$\frac{1}{2}$,GE=5,求AD的长.
 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.(1)求证:GE为⊙O的切线;
(2)若tanB=$\frac{1}{2}$,GE=5,求AD的长.
16.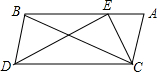 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )| A. | 107° | B. | 113° | C. | 115° | D. | 117° |
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题: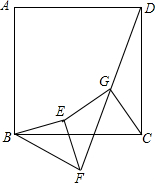 已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:
已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证: