题目内容
6. 如图,在平行四边形ABCD中,AD=2AB;CF平分∠BCD交AD于F,作CE⊥AB,垂足E在边AB上,连接EF.则下列结论:
如图,在平行四边形ABCD中,AD=2AB;CF平分∠BCD交AD于F,作CE⊥AB,垂足E在边AB上,连接EF.则下列结论:①F是AD的中点;②S△EBC=2S△CEF;
③EF=CF;④∠DFE=3∠AEF.
其中一定成立的是①③④.
(把所有正确结论的序号都填在横线上)
分析 由角平分线的定义和平行四边形的性质可证得CD=DF,则可求得F为AD的中点,可判断①;延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),结合直角三角形的性质可判断③;结合EF=FM,利用三角形的面积公式可判断②;在△DCF和△ECF中利用等腰三角形的性质、外角的性质及三角形内角和可得出∠DFE=3∠AEF,可判断④,可求得答案.
解答 解:
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DFC=∠BCF,
∵CF平分∠BCD,
∴∠BCF=∠DCF,
∴∠DFC=∠DCF,
∴CD=DF,
∵AD=2AB,
∴AD=2CD,
∴AF=FD=CD,即F为AD的中点,故①正确;
延长EF,交CD延长线于M,如图,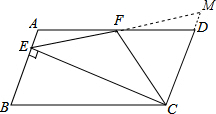
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
$\left\{\begin{array}{l}{∠A=∠FDM}\\{AF=DF}\\{∠AFE=∠DFM}\end{array}\right.$
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故③正确;
∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC,故②不正确;
设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故④正确;
综上可知正确的结论为①③④.
答案为:①③④.
点评 本题主要考查平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DME是解题关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| 试验次数 | 20 | 80 | 100 | 160 | 200 | 240 | 300 | 360 | 400 |
| “车”字朝上的频数 | 14 | 48 | 50 | 84 | 112 | 144 | 172 | 204 | 228 |
| 相应的频率 | 0.70 | 0.60 | 0.50 | 0.53 | 0.56 | 0.60 | 0.57 | 0.57 | 0.57 |
(2)根据上表,画出“车”字面朝上的频率的折线统计图;
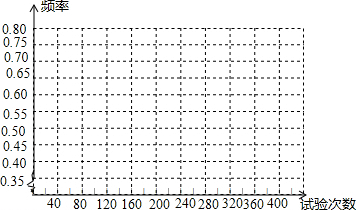
(3)如将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
| A. | 三角形的三个外角都是锐角 | |
| B. | 三角形的三个外角和至少有两个锐角 | |
| C. | 三角形的三个外角中没有锐角 | |
| D. | 三角形的三个外角中至少有一个锐角 |
 如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4) 如图,在△ABC中,AD是角平分线,DE∥AB交AC于点E,若∠DEC=100°,求∠ADE的度数.
如图,在△ABC中,AD是角平分线,DE∥AB交AC于点E,若∠DEC=100°,求∠ADE的度数.