题目内容
17. 如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)(1)将△ABC绕点O逆时针旋转90°,得到△A′B′C′,画出旋转后的图形;
(2)画出一条直线l使其将△ABC分为两部分,并且两部分的面积比为1:3;
(3)求sin∠ACB的值.
分析 (1)直接利用旋转的性质分别得出对应点位置,进而得出答案;
(2)直接利用底边分为1:3,即可得出两部分的面积比为1:3;
(3)首先得出BD,DC的长,再利用锐角三角三角函数关系得出答案.
解答 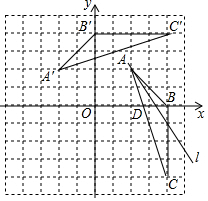 解:(1)如图所示:△A′B′C′,即为所求;
解:(1)如图所示:△A′B′C′,即为所求;
(2)如图所示:直线l,即为所求;
(3)由图象可得:A(2,2),C(4,-4),
设AC解析式为:y=kx+b,
则$\left\{\begin{array}{l}{2k+b=2}\\{4k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=8}\end{array}\right.$,
则直线AC的解析式为:y=-3x+8,
当y=0时,x=$\frac{8}{3}$,
则BD=4-$\frac{8}{3}$=$\frac{4}{3}$,
DC=$\sqrt{B{C}^{2}+B{D}^{2}}$=$\frac{4\sqrt{10}}{3}$,
故sin∠ACB=$\frac{BD}{DC}$=$\frac{\frac{4}{3}}{\frac{4\sqrt{10}}{3}}$=$\frac{\sqrt{10}}{10}$.
点评 此题主要考查了旋转变换以及锐角三角三角函数关系以及待定系数法求一次函数解析式,正确得出DC,BD的长是解题关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12.下列运算正确的是( )
| A. | a5+a5=a10 | B. | a6-a4=a24 | C. | a6•a4=a24 | D. | a8÷a5=a3 |
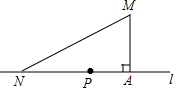 如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离.
如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离. 如图,AO⊥BC,∠3=∠2,且∠3的补角比它的余角的2倍多30°,求∠1的度数.
如图,AO⊥BC,∠3=∠2,且∠3的补角比它的余角的2倍多30°,求∠1的度数. 如图,在平行四边形ABCD中,AD=2AB;CF平分∠BCD交AD于F,作CE⊥AB,垂足E在边AB上,连接EF.则下列结论:
如图,在平行四边形ABCD中,AD=2AB;CF平分∠BCD交AD于F,作CE⊥AB,垂足E在边AB上,连接EF.则下列结论: