题目内容
16.已知x=2+$\sqrt{3}$是方程x2-5sinθ•x+1=0的一个根,且θ为锐角,求($\frac{3}{4}$tanθ-$\frac{5}{3}$cosθ)2016的值.分析 设方程的另一根为a,利用根与系数的关系式列出方程,求出a与sinθ的值,利用同角三角函数间的基本关系求出tanθ、cosθ的值即可.
解答 解:∵关于x的方程x2-5sinθ•x+1=0的一个根为2+$\sqrt{3}$,且θ为锐角,设另一根为a,
∴2+$\sqrt{3}$+a=5sinθ,a(2+$\sqrt{3}$)=1,
解得:a=2-$\sqrt{3}$,sinθ=$\frac{4}{5}$,
∴cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{3}{5}$,
则tanα=$\frac{sinθ}{cosθ}$=$\frac{4}{3}$.
∴($\frac{3}{4}$tanθ-$\frac{5}{3}$cosθ)2016=($\frac{3}{4}$×$\frac{4}{3}$-$\frac{5}{3}$×$\frac{3}{5}$)2016=0.
点评 此题考查了一元二次方程的解,根与系数的关系,以及同角三角函数间的基本关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.已知关于x的方程x2-kx-4=0的一个根为x=3,则实数k的值为( )
| A. | 5 | B. | 3 | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$. 如图,正方形ABCD与正方形EFGH边长相等,下列说法正确的个数有( )
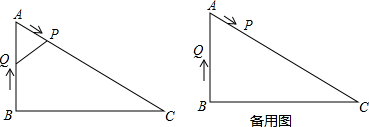
如图,正方形ABCD与正方形EFGH边长相等,下列说法正确的个数有( )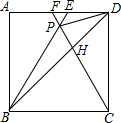 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论: