题目内容
6.抛物线y1=-2x2+2与y2=-(x-3)2+4在x轴上方(含与x轴的交点)的部分分别记作C1,C2,若直线y=$\frac{3}{5}$x+m与C1,C2共有至少3个不同的交点,则m的取值范围是-$\frac{3}{5}$≤m≤$\frac{409}{200}$.分析 根据已知条件得到抛物线y1=-2x2+2与x轴交于(-1,0),(1,0),顶点坐标(0,2),抛物线y2=-(x-3)2+4与x轴交于(1,0),(5,0),顶点坐标(3,4),于是若直线y=$\frac{3}{5}$x+m与y1相切时,求得m=$\frac{409}{200}$,若直线y=$\frac{3}{5}$x+m过(1,0)时,求得m=-$\frac{3}{5}$,于是得到结论.
解答 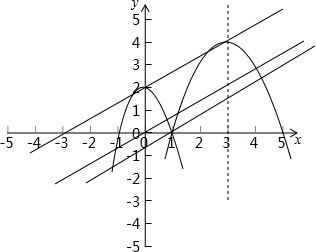 解:如图,∵抛物线y1=-2x2+2与x轴交于(-1,0),(1,0),顶点坐标(0,2),
解:如图,∵抛物线y1=-2x2+2与x轴交于(-1,0),(1,0),顶点坐标(0,2),
抛物线y2=-(x-3)2+4与x轴交于(1,0),(5,0),顶点坐标(3,4),
∴若直线y=$\frac{3}{5}$x+m与y1相切时,-2x2+2=$\frac{3}{5}$x+m,
∴△=($\frac{3}{5}$)2-4×(-2)×(m-2)=0,
∴m=$\frac{409}{200}$,若直线y=$\frac{3}{5}$x+m过(1,0)时,m=-$\frac{3}{5}$,
∴若直线y=$\frac{3}{5}$x+m与C1,C2共有至少3个不同的交点,则m的取值范围是-$\frac{3}{5}$≤m≤$\frac{409}{200}$,
故答案为:-$\frac{3}{5}$≤m≤$\frac{409}{200}$.
点评 本题主要考查二次函数与x轴的交点,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题有一定的难度.

练习册系列答案
相关题目
16.已知关于x的不等式组$\left\{\begin{array}{l}x-a>0\\ 7-2x>1\end{array}\right.$有且只有1个整数解,则a的取值范围是( )
| A. | a>1 | B. | 1≤a<2 | C. | 1<a≤2 | D. | a≤2 |
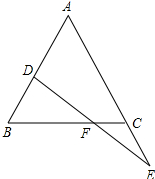 已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.
已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.