题目内容
10．
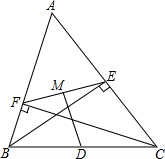如图，在△ABC中，BE、CF分别为边AC、AB上的高，D为BC的中点，DM⊥EF于M．求证：FM=EM．
分析 连接DE，DF，由直角三角形的性质得出DF=DE，再由DM⊥EF即可得出结论．
解答 
证明：连接DE，DF，
∵BE、CF分别为边AC、AB上的高，D为BC的中点，
∴DF=$\frac{1}{2}$BC，DE=$\frac{1}{2}$BC，
∴DF=DE，即△DEF是等腰三角形．
∵DM⊥EF，
∴点M时EF的中点，即FM=EM．
点评 本题考查的是直角三角形斜边上的中线，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，D点在BC上，∠1=∠2，∠1=35°，∠5=60°，求∠BAC，∠4的度数．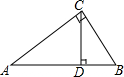
在直角三角形ABC中，∠ACB=90°，∠A、∠B、∠C的对边分别是a、b、c，CD⊥AB于点D，若AC=8，BC=6，求AB、AD、BD的长以及三角形ABC的面积．
如图，在△ABC中，D是BC边上的点，AD=DC，∠BAD=40°，∠C=35°，求证：△ABD是等腰三角形．