题目内容
19.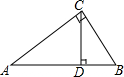 在直角三角形ABC中,∠ACB=90°,∠A、∠B、∠C的对边分别是a、b、c,CD⊥AB于点D,若AC=8,BC=6,求AB、AD、BD的长以及三角形ABC的面积.
在直角三角形ABC中,∠ACB=90°,∠A、∠B、∠C的对边分别是a、b、c,CD⊥AB于点D,若AC=8,BC=6,求AB、AD、BD的长以及三角形ABC的面积.
分析 根据题意直接利用勾股定理得出AB的长,再利用三角形面积求出DC的长,再利用勾股定理得出AD,BD的长.
解答 解:∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵CD⊥AB,
∴DC×AB=AC×BC,
则DC=$\frac{8×6}{10}$=$\frac{24}{5}$,
故AD=$\sqrt{{8}^{2}-(\frac{24}{5})^{2}}$=$\frac{32}{5}$,
则BD=10-$\frac{32}{5}$=$\frac{18}{5}$,
△ABC的面积为:$\frac{1}{2}$×8×6=24.
点评 此题主要考查了勾股定理以及三角形面积求法,根据题意得出DC的长是解题关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
7.如果两个数和为正数,则这两个数一定( )
| A. | 都是正数 | B. | 只有一个正数 | ||
| C. | 至少有一个是正数 | D. | 都不对 |
19.2014年12月30日,晋豫鲁铁路正式开通运营,据了解,晋豫鲁铁路是“晋煤外运”的新通道.线路起自山西兴县瓦塘站,终点是山东日照,全线长1260公里,横跨山西、河南、山东三省.总投资941亿元,941亿用科学记数法表示为( )
| A. | 941×108 | B. | 94.1×109 | C. | 9.41×1010 | D. | 9.41×1011 |
 如图,已知△ABC≌△DEF,∠B=∠E=90°,∠A=68°,AB=5,BC=9,CF=6.
如图,已知△ABC≌△DEF,∠B=∠E=90°,∠A=68°,AB=5,BC=9,CF=6.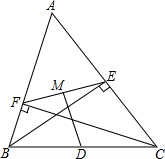 如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM.
如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM. 分别画出这个平房从正面,左面和上面看到的形状图.
分别画出这个平房从正面,左面和上面看到的形状图. A,C两地与海平面的相对高度如图所示,试用适当的方法表示A,B,C三地的高度.
A,C两地与海平面的相对高度如图所示,试用适当的方法表示A,B,C三地的高度.