题目内容
2.已知方程x2-5x-6=0的根是x1和x2,不解方程,求下列式子的值.(1)${x}_{1}^{2}$+${x}_{2}^{2}$+x1x2;
(2)$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$.
分析 根据根与系数的关系得到x1+x2=5,x1•x2=-6.
(1)把原式变形得到x1+x2)2-x1•x2,然后利用整体代入的方法计算;
(2)把原式变形得到$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=5,x1•x2=-6,
(1)原式=(x1+x2)2-x1•x2=25+6=31;
(2)原式=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{37}{6}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.如果两个数和为正数,则这两个数一定( )
| A. | 都是正数 | B. | 只有一个正数 | ||
| C. | 至少有一个是正数 | D. | 都不对 |
2.一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
(1)请你根据上述统计数据,把下面的图和表补充完整.
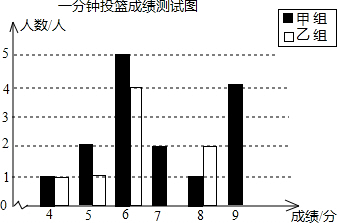
(2)下面是小明和小聪的一段对话.请你根据(1)中的表,写出两条支持小聪的观点的理由.
小明:我认为,因为甲组的优秀率高于乙组,所以甲组的成绩更好于乙组;
小聪:我认为:乙组的成绩要好于甲组.
| 成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
| 甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
| 乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |

| 统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
| 甲组 | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
| 乙组 | 6.8 | 1.76 | 7 | 86.7% | 13.3% |
小明:我认为,因为甲组的优秀率高于乙组,所以甲组的成绩更好于乙组;
小聪:我认为:乙组的成绩要好于甲组.
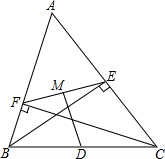 如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM.
如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM. 分别画出这个平房从正面,左面和上面看到的形状图.
分别画出这个平房从正面,左面和上面看到的形状图.