题目内容
5.解下列方程:(1)4(x-3)2 -25(x-2)2=0;
(2)(2x-1)2+3(1-2x)=0.
分析 (1)分解因式,即可得出两个一元一次方程,求出方程的解即可.
(2)分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)4(x-3)2 -25(x-2)2=0;
【2(x-3)+5(x-2)】【2(x-3)-5(x-2)】=0,
(7x-16)(-3x+4)=0
7x-16=0,-3x+4=0,
x1=$\frac{16}{7}$,x2=$\frac{4}{3}$;
(2)(2x-1)2+3(1-2x)=0,
(2x-1)(2x-1-3)=0,
2x-1=0,2x-4=0,
x1=$\frac{1}{2}$,x2=2.
点评 本题考查了解一元二次方程的应用,关键是能把一元二次方程转化成一元一次方程.

练习册系列答案
相关题目
5.已知xy>0,将$\sqrt{-\frac{y}{{x}^{2}}}$化为最简二次根式为( )
| A. | $\frac{\sqrt{y}}{x}$ | B. | $\frac{\sqrt{-y}}{x}$ | C. | $\frac{-\sqrt{y}}{x}$ | D. | $\frac{-\sqrt{-y}}{x}$ |
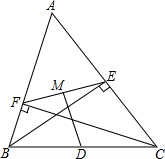 如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM.
如图,在△ABC中,BE、CF分别为边AC、AB上的高,D为BC的中点,DM⊥EF于M.求证:FM=EM. 分别画出这个平房从正面,左面和上面看到的形状图.
分别画出这个平房从正面,左面和上面看到的形状图.