题目内容
19.(1)解方程组:$\left\{{\begin{array}{l}{x=y+1}\\{2x-y=3}\end{array}}\right.$(2)解不等式组:$\left\{{\begin{array}{l}{3x-5≤x+6}\\{\frac{x-1}{3}<\frac{x}{2}-1}\end{array}}\right.$,并将解集在数轴上表示出来.
分析 (1)把①代入②得出2(y+1)-y=3,求出y,把y=1代入①求出x即可;
(2)先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
解答 解:(1)$\left\{\begin{array}{l}{x=y+1①}\\{2x-y=3②}\end{array}\right.$
把①代入②得:2(y+1)-y=3,
解得:y=1,
把y=1代入①得:x=1+1=2,
所以方程组的解为$\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$;
(2)$\left\{\begin{array}{l}{3x-5≤x+6①}\\{\frac{x-1}{3}<\frac{x}{2}-1②}\end{array}\right.$
∵解不等式①得:x≤5.5,
解不等式②得:x>4,
∴不等式组的解集为 4<x≤5.5,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集,解二元一次方程组等知识点,能把二元一次方程组转化成一元一次方程是解(1)的关键,能求出不等式组的解集是解(2)的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
4. 如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )
如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )
 如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )
如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
11.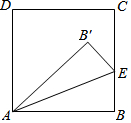 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}y-x=48\\ y+x=90\end{array}\right.$ | B. | $\left\{\begin{array}{l}y-x=48\\ y=2x\end{array}\right.$ | C. | $\left\{\begin{array}{l}y-x=48\\ y+2x=90\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=48\\ y+2x=90\end{array}\right.$ |
8. 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )| A. | $\frac{4}{3}$ | B. | -1 | C. | -5 | D. | -8 |