题目内容
9.自从北京获得2022年第24届冬季奥林匹克运动会主办权以来,某纪念章经销商预测印有“冬季奥林匹克运动会”标志的甲、乙两种纪念章能够畅销,用16500元购进了甲种纪念章,用44000元购进了乙种纪念章,由于乙种纪念章的单价是甲种纪念章单价的4倍,实际购得甲种纪念章的数量比乙种纪念章的数量多100个.(1)求购进甲、乙两种纪念章的单价各多少元?
(2)如果要求每件商品在销售时的利润为20%,那么甲、乙两种纪念章每件的销售价各是多少元?
(3)在(2)的条件下,如果甲种纪念章的进价降低了,但售价保持不变,从而使销售甲种纪念章的利润至少提高了5%,那么此时每个甲种纪念章的进价最多是多少元?
分析 (1)根据题意可以列出相应的分式方程,从而可以求得购进甲、乙两种纪念章的单价;
(2)根据(1)中的结果和题意可以求得甲、乙两种纪念章每件的销售价;
(3)根据题意可以列出相应的不等式,从而可以解答本题.
解答 解:(1)设甲种纪念章的单价是x元,
$\frac{16500}{x}-100=\frac{44000}{4x}$,
解得,x=55,
经检验,x=55是原分式方程的解,
∴4x=220,
答:购进甲、乙两种纪念章的单价分别是55元、220元;
(2)由题意可得,
甲种纪念章的单价是:55(1+20%)=66(元),
乙种纪念章的单价是:220(1+20%)=264(元),
答:甲、乙两种纪念章每件的销售价分别是66元、264元;
(3)设每个甲种纪念章的进价是x元,
x(1+25%)≤66,
解得,x≤52.8,
∴此时每个甲种纪念章的进价最多是52.8元,
答:此时每个甲种纪念章的进价最多是52.8元.
点评 本题考查分式方程的应用、一元一次不等式的应用,解答本题的关键是明确题意,列出相应的分式方程和一元一次不等式.

练习册系列答案
相关题目
17.若$\sqrt{10201}$=101,则$\sqrt{102.01}$等于( )
| A. | 1.01 | B. | 10.1 | C. | 101 | D. | 1.0201 |
4.桥梁上的拉杆,电视塔的底座,都是三角形结构,而活动挂架是四边形结构,这是分别利用三角形和四边形的( )
| A. | 稳定性,稳定性 | B. | 稳定性,不稳定性 | ||
| C. | 不稳定性,稳定性 | D. | 不稳定性,不稳定性 |
14.为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:

身高情况分组表(单位:cm)
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在B组,中位数在C组;
(2)样本中,女生身高在E组的人数有2人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?

身高情况分组表(单位:cm)
| 组别 | 身高 |
| A | x<160 |
| B | 160≤x<165 |
| C | 165≤x<170 |
| D | 170≤x<175 |
| E | x≥175 |
(1)样本中,男生的身高众数在B组,中位数在C组;
(2)样本中,女生身高在E组的人数有2人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?
18.阅读下列材料:
2016年人均阅读16本书!
2017年4月23日“世界读书日”之前,国际网络电商亚马逊发布了“亚马逊中国2017全民阅读报告”.报告显示,大部分读者已养成一定的阅读习惯,阅读总量在10本以上的占56%,而去年阅读总量在10本以上的占48%.
京东图书也发布了2016年度图书阅读报告.根据京东图书文娱业务部数据统计,2016年销售纸书人均16册,总量叠在一起相当于15000个帝国大厦的高.
(1)在亚马逊这项调查中,以每年有效问卷1.4万份来计,2017年阅读量十本以上的人数比去年增加了1120人;
(2)小雨作为学校的图书管理员,根据初二年级每位同学本学期的借书记录,对各个班借阅的情况作出了统计,并绘制统计图表如下:
初二年级图书借阅分类统计扇形图
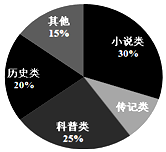
初二年级各班图书借阅情况统计表
①全年级140名同学中有科技社团成员40名,他们人均阅读科普类书籍1.5本,年级其他同学人均阅读科普类书籍1.08本,请你计算全年级人均阅读科普类书籍的数量,再通过计算补全统计表;
②在①的条件下,若要推荐初二某个班级为本学期阅读先进集体,你会推荐哪个班,请写出你的理由.
2016年人均阅读16本书!
2017年4月23日“世界读书日”之前,国际网络电商亚马逊发布了“亚马逊中国2017全民阅读报告”.报告显示,大部分读者已养成一定的阅读习惯,阅读总量在10本以上的占56%,而去年阅读总量在10本以上的占48%.
京东图书也发布了2016年度图书阅读报告.根据京东图书文娱业务部数据统计,2016年销售纸书人均16册,总量叠在一起相当于15000个帝国大厦的高.
(1)在亚马逊这项调查中,以每年有效问卷1.4万份来计,2017年阅读量十本以上的人数比去年增加了1120人;
(2)小雨作为学校的图书管理员,根据初二年级每位同学本学期的借书记录,对各个班借阅的情况作出了统计,并绘制统计图表如下:
初二年级图书借阅分类统计扇形图

初二年级各班图书借阅情况统计表
| 班级 | 1 | 2 | 3 | 4 |
| 人数 | 35 | 35 | 34 | 36 |
| 借阅总数(本) | 182 | 165 | 143 | |
| 中位数 | 5 | 6 | 5 | 5 |
②在①的条件下,若要推荐初二某个班级为本学期阅读先进集体,你会推荐哪个班,请写出你的理由.
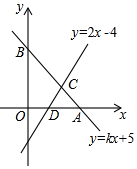 已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.
已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.