题目内容
7.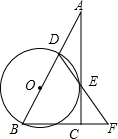 如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.
如图,在Rt△ABC中,△ACB=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长,与BC的延长线交于点F.(1)求证:BD=BF;
(2)若BC=6,AB=12,求⊙O的面积.
分析 (1)连接OE,由AC是⊙O的切线,得OE⊥AC,再根据题意得OE∥BF,则∠OED=∠F,OD=OE,从而得出∠F=∠BDF,即BD=NF;
(2)设⊙O的半径为r,由OE∥BF,可证明△AOE∽△ABC,根据相似三角形的性质得到$\frac{AO}{AB}=\frac{OE}{BC}$,即可求得r,进而得出⊙O的面积.
解答 (1)证明:连接OE,∵AC是⊙O的切线,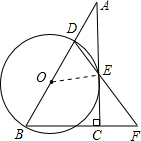
∴OE⊥AC
又∵∠ACB=90°,
∴OE∥BF,
∴∠OED=∠F,
∵OD=OE,
∴∠OED=∠BDF,
∴∠F=∠BDF,
即BD=BF;
(2)解:设⊙O的半径为r,则AO=12-r,
∵OE∥BF,
∴△AOE∽△ABC,
∴$\frac{AO}{AB}=\frac{OE}{BC}$,即$\frac{12-r}{12}=\frac{r}{6}$,
解得r=4,
∴S⊙O=42π=16π.
点评 本题考查了切线的性质,相似三角形的判定和性质,本题涉及的知识点:两直线平行,等腰三角形的判定、三角形相似、圆的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.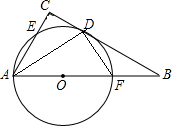 如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证:
如图,在△ABC中,∠C=90°,∠B=30°,点O在AB上,以O为圆心,OA为半径的⊙O与BC相切于点D,与AC,AB分别交于点E、F,连接AD和DF.求证: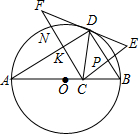 已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证:
已知:如图,AB是⊙O的直径,点C是直径AB上一点,点D在⊙O上,CE⊥CF,BD垂直平分CE于点P,CF交AD于点K,交⊙O于点N.求证: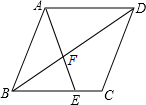 如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.
如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.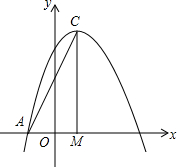 如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.
如图,已知抛物线y=-x2+bx+c与x轴的一个交点为A(-1,0),对称轴为直线x=1.