题目内容
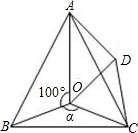 如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.
如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.(1)求证:△COD是等边三角形;
(2)探究:当α为多少度时,△AOD是等腰三角形?
考点:等边三角形的判定与性质,等腰三角形的判定
专题:
分析:(1)由旋转的性质可知CO=CD,∠OCD=60°,可判断:△COD是等边三角形;
(2)由(1)可知∠COD=60°,当α=130°时,∠ADO=∠ADC-∠CDO,可判断△AOD为等腰三角形.
(2)由(1)可知∠COD=60°,当α=130°时,∠ADO=∠ADC-∠CDO,可判断△AOD为等腰三角形.
解答:(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,CO=CD,
∴△OCD是等边三角形;
(2)解:△AOD为直角三角形.
理由:∵△COD是等边三角形.
∴∠COD=∠ODC=60°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α,
∴∠ADO=∠ADC-∠CDO=α-60°
∠ABO+∠α+∠COD+∠AOD=360°
∴α+∠AOD=360°-100°-60°=200°
∠ADO+∠AOD=140°
∠ADO=AOD=70°,△AOD是等腰三角形,
∴α=∠ADC=ADO+∠ODC=130°时,△AOD是等腰三角形.
∴∠OCD=60°,CO=CD,
∴△OCD是等边三角形;
(2)解:△AOD为直角三角形.
理由:∵△COD是等边三角形.
∴∠COD=∠ODC=60°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α,
∴∠ADO=∠ADC-∠CDO=α-60°
∠ABO+∠α+∠COD+∠AOD=360°
∴α+∠AOD=360°-100°-60°=200°
∠ADO+∠AOD=140°
∠ADO=AOD=70°,△AOD是等腰三角形,
∴α=∠ADC=ADO+∠ODC=130°时,△AOD是等腰三角形.
点评:本题考查了旋转的性质,等边三角形的判定,等腰三角形的性质,关键是利用旋转前后,对应边相等,对应角相等解题.

练习册系列答案
相关题目
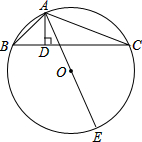 如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径.
如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O的直径. 如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程: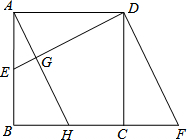 如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.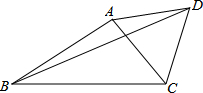 如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长.
如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长. 画y=2x+1的图象.
画y=2x+1的图象.