题目内容
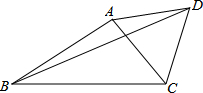 如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长.
如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长.考点:全等三角形的判定与性质,等边三角形的性质,勾股定理
专题:计算题
分析:以AB为边作等边三角形AEB,连接CE,如图所示,由三角形ABE与三角形ACD都为等边三角形,利用等边三角形的性质得到AE=AB,AD=AC,且∠EAB=∠DAC=60°,利用等式的性质得到夹角相等,利用SAS得到三角形EAC与三角形BAD全等,利用全等三角形的对应边相等得到EC=BD=5,再由∠EBA+∠ABC=∠EBC,得到三角形EBC为直角三角形,利用勾股定理求出BC的长即可.
解答: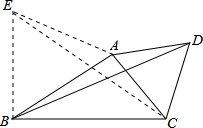 解:以AB为边作等边三角形AEB,连接CE,如图所示,
解:以AB为边作等边三角形AEB,连接CE,如图所示,
∵△ABE与△ACD都为等边三角形,
∴∠EAB=∠DAC=60°,AE=AB,AD=AC,
∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS),
∴BD=EC=5,
∵∠EBA=60°,∠ABC=30°,
∴∠EBC=90°,
在Rt△EBC中,EC=5,EB=3,
根据勾股定理得:BC=
=4.
 解:以AB为边作等边三角形AEB,连接CE,如图所示,
解:以AB为边作等边三角形AEB,连接CE,如图所示,∵△ABE与△ACD都为等边三角形,
∴∠EAB=∠DAC=60°,AE=AB,AD=AC,
∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
|
∴△EAC≌△BAD(SAS),
∴BD=EC=5,
∵∠EBA=60°,∠ABC=30°,
∴∠EBC=90°,
在Rt△EBC中,EC=5,EB=3,
根据勾股定理得:BC=
| 52-32 |
点评:此题考查了全等三角形的判定与性质,等边三角形的性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列运算中,正确的是( )
| A、x2+x2=x4 |
| B、x6÷x2=x3 |
| C、x2•x4=x6 |
| D、(3x2)2=6x4 |

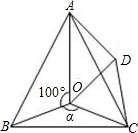 如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.
如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.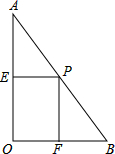 如图,在Rt△ABC中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一动点,PE⊥AO于点E,PF⊥BO于点F,设PE=x,矩形PFOE的面积为s.
如图,在Rt△ABC中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一动点,PE⊥AO于点E,PF⊥BO于点F,设PE=x,矩形PFOE的面积为s.