题目内容
如图，已知AB∥DC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E．试说明AD∥BC．完成推理过程：∵AB∥DC（已知）
∴∠1=
∵AE平分∠BAD（已知）
∴∠1=∠2 （角平分线的定义）
∴
∵∠CFE=∠E（已知）
∴∠2=
∴AD∥BC （
考点：平行线的判定与性质
专题：推理填空题
分析：由AB与CD平行，利用两直线平行内错角相等得到一对角相等，再由AE为角平分线得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得证．
解答：证明：∵AB∥DC（已知）
∴∠1=∠CFE（两直线平行，同位角相等）
∵AE平分∠BAD（已知）
∴∠1=∠2（角平分线的定义）
∴∠CFE=∠2（等量代换）
∵∠CFE=∠E（已知）
∴∠2=∠E（等量代换）
∴AD∥BC（内错角相等，两直线平行）．
故答案为：∠CFE；两直线平行，内错角相等；∠CFE；∠2；等量代换；∠E；内错角相等，两直线平行．
∴∠1=∠CFE（两直线平行，同位角相等）
∵AE平分∠BAD（已知）
∴∠1=∠2（角平分线的定义）
∴∠CFE=∠2（等量代换）
∵∠CFE=∠E（已知）
∴∠2=∠E（等量代换）
∴AD∥BC（内错角相等，两直线平行）．
故答案为：∠CFE；两直线平行，内错角相等；∠CFE；∠2；等量代换；∠E；内错角相等，两直线平行．
点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
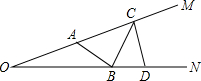如图，∠MON=20°，A为射线OM上一点，OA=4，D为射线ON上一点，OD=8，C为射线AM上任意一点，B是线段OD上任意一点，那么折线ABCD的长AB+BC+CD的最小值是
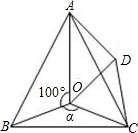如图，点O是等边△ABC内一点，∠AOB=10°，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连结OD．