题目内容
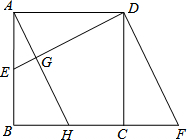 如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.(1)求证:△ADE≌△CDF.
(2)把△DCF向左平移,使DC与AB重合,得△ABH,AH交ED于点G.请判断AH与ED的位置关系,并说明理由.
(3)求AG的长.
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)根据正方形的性质可得AD=DC,∠BAD=∠DCF=90°,然后利用“边角边”证明△ADE和△CDF全等即可;
(2)根据全等三角形对应角相等可得∠1=∠2,再根据平移的性质可得∠2=∠3,从而得到∠1=∠3,再求出∠1+∠4=90°,然后求出∠AGD=90°,再根据垂直的定义证明即可;
(3)根据中点的定义求出AE,再利用勾股定理列式求出DE,然后根据△ADE的面积列出方程求解即可.
(2)根据全等三角形对应角相等可得∠1=∠2,再根据平移的性质可得∠2=∠3,从而得到∠1=∠3,再求出∠1+∠4=90°,然后求出∠AGD=90°,再根据垂直的定义证明即可;
(3)根据中点的定义求出AE,再利用勾股定理列式求出DE,然后根据△ADE的面积列出方程求解即可.
解答:解:(1)∵四边形ABCD是正方形,
∴AD=DC,∠BAD=∠DCF=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS);
(2)AH⊥ED.
理由如下:如图,∵△ADE≌△CDF,
∴∠1=∠2,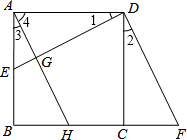
由平移性质,∠2=∠3,
∴∠1=∠3,
∵∠3+∠4=∠BAD=90°,
∴∠1+∠4=90°,
∴∠AGD=90°,
∴AH⊥ED;
(3)∵正方形ABCD的边长是2,E是AB的中点,
∴AE=
×2=1,AD=2,
∴ED=
=
=
,
∴S△AED=
AE•AD=
ED•AG,
即
×1×2=
×
•AG,
解得AG=
.
∴AD=DC,∠BAD=∠DCF=90°,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(SAS);
(2)AH⊥ED.
理由如下:如图,∵△ADE≌△CDF,
∴∠1=∠2,

由平移性质,∠2=∠3,
∴∠1=∠3,
∵∠3+∠4=∠BAD=90°,
∴∠1+∠4=90°,
∴∠AGD=90°,
∴AH⊥ED;
(3)∵正方形ABCD的边长是2,E是AB的中点,
∴AE=
| 1 |
| 2 |
∴ED=
| AE2+AD2 |
| 12+22 |
| 5 |
∴S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
解得AG=
2
| ||
| 5 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,平移的性质,勾股定理,三角形的面积,(3)利用三角形的面积列出方程求解是常用的方法,要熟练掌握并灵活运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
下列计算正确的是( )
| A、(a2)3=a5 |
| B、a6÷a3=a2 |
| C、a2•a=a3 |
| D、(a-b)2=a2-b2 |
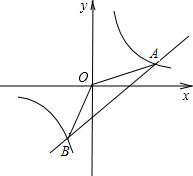 如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2=
如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2=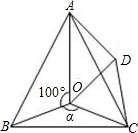 如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.
如图,点O是等边△ABC内一点,∠AOB=10°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连结OD.