题目内容
20.若双曲线y=$\frac{1-k}{x}$的图象在第一、三象限,则k的取值范围为( )| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
分析 若反比例函数 y=$\frac{1-k}{x}$的图象经过第一、三象限,即反比例系数1-k>0,从而求得k的范围.
解答 解:∵函数y=$\frac{1-k}{x}$的图象在第一、三象限内,
∴1-k>0,
解得k<1,
故选D.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)的性质:①当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.

练习册系列答案
相关题目
11.反比例函数y=$\frac{k}{x}$的图象生经过点(1,-2),则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
8.在Rt△ABC中,若各边长都扩大3倍,则锐角A的正弦值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小到原来的$\frac{1}{3}$ | D. | 不能确定 |
15.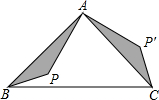 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
5.有如下四个事件:①篮球队员在罚球线上投篮一次,未投中;②任意画一个圆的内接四边形,这个四边形的对角互补;③经过有交通信号灯的路口,遇到红灯;④三角形的外心落在三角形的内部.上述事件中是随机事件的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
12.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{2{x}^{2}}$ | B. | $\sqrt{5}$ | C. | $\sqrt{8}$ | D. | $\sqrt{\frac{1}{x}}$ |
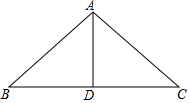 如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)