题目内容
19.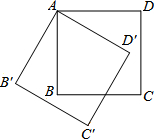 如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )| A. | $\frac{2}{3}$πcm | B. | $\frac{2\sqrt{2}}{3}$πm | C. | $\frac{2\sqrt{3}}{3}$cm | D. | $\frac{2\sqrt{5}}{3}$cm |
分析 如图,作辅助线;首先求出AC的长度,然后运用弧长公式即可解决问题.
解答 解:如图,连接AC、A′C.
∵四边形ABCD为边长为4的正方形,
∴∠B=90°,AB=BC=4,
由勾股定理得:AC=4$\sqrt{2}$,
由题意得:∠CAC′=30°,
∴点C的旋转路径长=$\frac{30π•4\sqrt{2}}{180}=\frac{2\sqrt{2}}{3}π$,
故选B
点评 该题以正方形为载体,以旋转变换为方法,以考查旋转变换的性质为核心构造而成;解题的关键是将求点C的旋转路径长问题,转化为求弧长问题.

练习册系列答案
相关题目
7.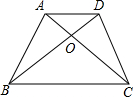 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
14.下列说法:①球有1个面;②同一平面内的两点,可以确定一条直线;③两点之间,线段最短;④射线没有端点,其中不正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.若一元二次方程(2m+6)x2+m2-9=0的常数项是0,则m等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 9 |
11.反比例函数y=$\frac{k}{x}$的图象生经过点(1,-2),则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
8.在Rt△ABC中,若各边长都扩大3倍,则锐角A的正弦值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小到原来的$\frac{1}{3}$ | D. | 不能确定 |
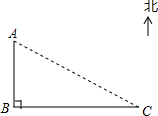 如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?
如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?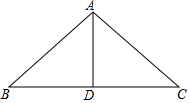 如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)