题目内容
3.有黑白两种小球若干只,且同色小球的质量均相同,在如图所示的两次称量中天平均恰好平衡,若每只砝码的质量均为5克,则每只黑球和白球的质量各是多少克?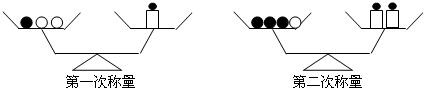
分析 设每只黑球的质量为x克,每只白球的质量为y克,根据“1只黑球、2只白球的总质量为5克,3只黑球、1只白球的总质量为10克”即可得出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:设每只黑球的质量为x克,每只白球的质量为y克,
根据题意得:$\left\{\begin{array}{l}{x+2y=5}\\{3x+y=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$.
答:每只黑球的质量为3克,每只白球的质量为1克.
点评 本题考查了二元一次方程组的应用,根据天平两边的质量相当列出关于x、y的二元一次方程组是解题的关键.

练习册系列答案
相关题目
8.已知|2017-a|+$\sqrt{a-2018}$=a,则a-20172的值为( )
| A. | 2017 | B. | 2018 | C. | 20172 | D. | 20182 |
15.明明家离学校1500米,其中有一段为上坡路.另一段为下坡路,某天他去学校共用了12分钟,假设明明上坡路的平均速度是5千米/时,下坡路的平均速度是8千米/时.若设明明上坡路用了x分钟,下坡路用了y分钟,根据题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=12}\\{5x+8y=1500}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+8y=1.5}\\{x+y=12}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x-\frac{2}{15}y=1.5}\end{array}\right.$ |
12.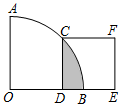 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | 2π-2 | C. | 4π-4 | D. | 4π-8 |
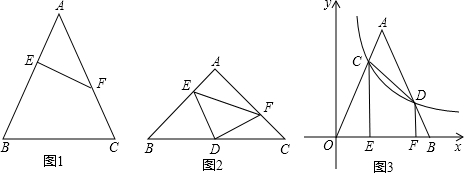
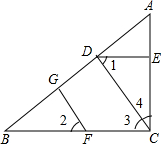 如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB.
如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB. 如图,已知∠1=∠2,∠A=∠F,试判断∠C与∠D的大小关系,说明理由.
如图,已知∠1=∠2,∠A=∠F,试判断∠C与∠D的大小关系,说明理由.