题目内容
6.计算或解方程(1)(x-1)2=4
(2)-2(x+1)3=54
(3)$\sqrt{5}$(-1+$\frac{\sqrt{2}}{\sqrt{5}}$)-|2$\sqrt{2}$-$\sqrt{5}$|
(4)|-1-$\sqrt{2}$|-|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}-\sqrt{2}$|
分析 (1)根据平方根的求法,求出x的值是多少即可.
(2)根据立方根的求法,求出x的值是多少即可.
(3)应用乘法分配律,求出算式的值是多少即可.
(4)根据绝对值的含义和求法,求出算式的值是多少即可.
解答 解:(1)∵(x-1)2=4,
∴x-1=±2,
解得x=3或-1.
(2)∵-2(x+1)3=54,
∴x+1=-3,
解得x=-4.
(3)$\sqrt{5}$(-1+$\frac{\sqrt{2}}{\sqrt{5}}$)-|2$\sqrt{2}$-$\sqrt{5}$|
=-$\sqrt{5}$+$\sqrt{5}$×$\frac{\sqrt{2}}{\sqrt{5}}$-2$\sqrt{2}$+$\sqrt{5}$
=-$\sqrt{5}$+$\sqrt{2}$-2$\sqrt{2}$+$\sqrt{5}$
=-$\sqrt{2}$
(4)|-1-$\sqrt{2}$|-|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}-\sqrt{2}$|
=1+$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$+$\sqrt{3}-\sqrt{2}$
=1+$\sqrt{2}$
点评 此题主要考查了实数的运算,平方根、立方根的求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
相关题目
7.随着行政区划调整,2017年我区计划新建续建主次干道项目25个,全年计划完成交通投资19.79亿元,其中19.79亿元用科学记数法可表示为( )
| A. | 1.979×107元 | B. | 1.979×108元 | C. | 1.979×109元 | D. | 1.979×1010元 |
1.M国股民吉姆上周末买进某公司月股票1000股,每股27 元,下表为本周内每日该股的涨跌情况 (星期六、日股市休市) (单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价多少元?最低价是多少元?
(3)已知吉姆买进股票时付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +6 | +6.5 | -1 | -2.5 | -6 |
(2)本周内每股最高价多少元?最低价是多少元?
(3)已知吉姆买进股票时付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
15.明明家离学校1500米,其中有一段为上坡路.另一段为下坡路,某天他去学校共用了12分钟,假设明明上坡路的平均速度是5千米/时,下坡路的平均速度是8千米/时.若设明明上坡路用了x分钟,下坡路用了y分钟,根据题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=12}\\{5x+8y=1500}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+8y=1.5}\\{x+y=12}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x-\frac{2}{15}y=1.5}\end{array}\right.$ |
16.关于x,y的二元一次方程组$\left\{\begin{array}{l}x+y=9k\\ x-y=5k\end{array}\right.$的解也是二元一次方程2x+3y=6的解,则k的值为( )
| A. | $\frac{3}{10}$ | B. | $\frac{10}{3}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{10}{3}$ |
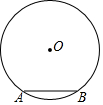 如图,⊙O的半径为1,AB是⊙O的一条弦,且AB=1,则弦AB所对的圆周角的度数为30°或150°.
如图,⊙O的半径为1,AB是⊙O的一条弦,且AB=1,则弦AB所对的圆周角的度数为30°或150°.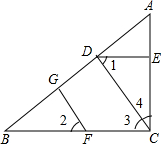 如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB.
如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB. 如图,已知∠1=∠2,∠A=∠F,试判断∠C与∠D的大小关系,说明理由.
如图,已知∠1=∠2,∠A=∠F,试判断∠C与∠D的大小关系,说明理由.