题目内容
12. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
分析 利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;利用勾股定理得出GE2=CG2+CE2,进而求出BG即可.
解答 解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=GF,
∵E是边CD的中点,
∴DE=CE=3,
设BG=x,则CG=6-x,GE=x+3,
∵GE2=CG2+CE2
∴(x+3)2=(6-x)2+32,
解得 x=2
∴BG=2.
故答案为:2.
点评 此题主要考查了全等三角形的判定和性质,勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.

练习册系列答案
相关题目
2.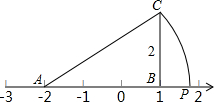 如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )
如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )
 如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )
如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )| A. | $\sqrt{13}$ | B. | $\sqrt{13}$-2 | C. | $\sqrt{13}$-3 | D. | 4-$\sqrt{13}$ |
7.下列各题去括号所得结果正确的是( )
| A. | x2-(x-y+2z)=x2-x+y+2z | B. | x-[-y+(-3x+1)]=x+y+3x-1 | ||
| C. | 3x-[5x-(x-1)]=3x-5x-x+1 | D. | (x-1)-(x2-2)=x-1-x2-2 |
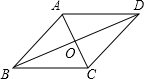 如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可) 已知:如图,BC∥AD,∠A=∠B.
已知:如图,BC∥AD,∠A=∠B.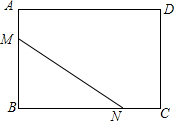 如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.