题目内容
20.当x≠-$\frac{3}{2}$时,分式$\frac{2x-3}{2x+3}$有意义;当x1时,分式$\frac{|x|-1}{{{x^2}+2x+1}}$的值为零.分析 根据分母不为零分式有意义,分子为零且分母不为零分式的值为零,可得答案.
解答 解:由分式$\frac{2x-3}{2x+3}$有意义,得
2x+3≠0,解得x≠-$\frac{3}{2}$,
由分式$\frac{|x|-1}{{{x^2}+2x+1}}$的值为零得
|x|-1=0且x2+2x+1≠0.
解得x=1.
故答案为:≠-$\frac{3}{2}$,1.
点评 本题考查了分式值为零的条件,利用分子为零且分母不为零分式的值为零得出|x|-1=0且x2+2x+1≠0是解题关键.

练习册系列答案
相关题目
10.有四条线段,长度分别是2cm,3cm,4cm,5cm,从中任取三条,能构成三角形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.点M(1-m,3-m)在x轴上,则点M坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
15.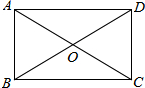 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AD |
 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2. 如图,直线a∥b,∠DAC=28°,∠CBE=50°,则∠ACB=78°.
如图,直线a∥b,∠DAC=28°,∠CBE=50°,则∠ACB=78°. 如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由.
如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由.