题目内容
4.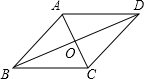 如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
如图,四边形ABCD的对角线互相平分,若再补充一个条件能使四边形ABCD成为矩形,则这个条件是AC=BD(答案不唯一)(只填一个条件即可)
分析 由四边形ABCD的对角线互相平分,可得四边形ABCD是平行四边形,再添加AC=BD,可根据对角线相等的平行四边形是矩形即可得出结论.
解答 解:可添加AC=BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形.
故答案为:AC=BD(答案不唯一).
点评 此题主要考查了矩形的判定,关键是矩形的判定:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
15.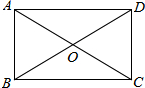 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AD |
13.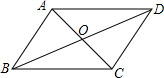 如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
 如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )| A. | 10 | B. | 11 | C. | 12 | D. | 22 |
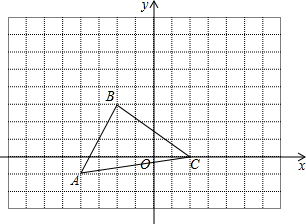 如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.
如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2. 如图,直线a∥b,∠DAC=28°,∠CBE=50°,则∠ACB=78°.
如图,直线a∥b,∠DAC=28°,∠CBE=50°,则∠ACB=78°.