题目内容
2.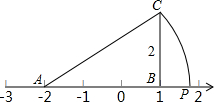 如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )
如图,数轴上A表示数-2,过数轴上表示1的点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,那么数轴上点P所表示的数是( )| A. | $\sqrt{13}$ | B. | $\sqrt{13}$-2 | C. | $\sqrt{13}$-3 | D. | 4-$\sqrt{13}$ |
分析 首先在直角三角形中,利用勾股定理可以求出线段CA的长度,然后根据AC=AP即可求出AP的长度,接着可以求出数轴上点P所表示的数.
解答 解:∵CA=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴AC=AP=$\sqrt{13}$,
∴P到原点的距离是$\sqrt{13}$-2,且P在原点右侧.
∴点P所表示的数是$\sqrt{13}$-2.
故选:B.
点评 此题主要考查了实数与数轴之间的对应关系,首先正确根据数在数轴上的位置判断数的符号以及绝对值的大小,再根据运算法则进行判断.

练习册系列答案
相关题目
10.有四条线段,长度分别是2cm,3cm,4cm,5cm,从中任取三条,能构成三角形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
17.在实数0,π,$\frac{1}{3}$,$\sqrt{2}$,-$\sqrt{9}$中,无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.点M(1-m,3-m)在x轴上,则点M坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
 将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.
将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.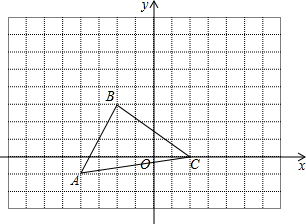 如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1.
如图,三角形ABC中,任意移动P(x0,y0)经平移后对应点为P0(x0+5,y0+3).将三角形ABC作同样的平移后得到三角形A1B1C1. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.