题目内容
2.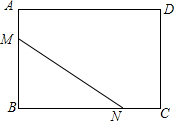 如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
如图,在矩形ABCD中,AB=6,AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于3$\sqrt{5}$.
分析 设AM=x,表示出EM=BM=6-x,AE=2x,再利用勾股定理列出方程求出x,然后求出BM,AE,过点N作NF⊥AD于F,求出△AME和△FEN,再利用相似三角形对应边成比例列式求解即可.
解答  解:设AM=x,则EM=BM=6-x,AE=2AM=2x,
解:设AM=x,则EM=BM=6-x,AE=2AM=2x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴在Rt△AME中,由勾股定理得,AM2+AE2=EM2,
即x2+(2x)2=(6-x)2,
整理得,x2+3x-9=0,
解得x1=$\frac{-3+3\sqrt{5}}{2}$,x2=$\frac{-3-3\sqrt{5}}{2}$(舍去),
所以,BM=6-$\frac{-3+3\sqrt{5}}{2}$=$\frac{15-3\sqrt{5}}{2}$,AE=-3+3$\sqrt{5}$,
过点N作NF⊥AD于F,易求△AME∽△FEN,
所以,$\frac{AE}{FN}=\frac{EM}{EN}$,
即$\frac{-3+3\sqrt{5}}{6}=\frac{\frac{15-3\sqrt{5}}{2}}{EN}$,
解得EN=3$\sqrt{5}$.
故答案为:3$\sqrt{5}$.
点评 本题考查了翻折变换的性质,勾股定理,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于利用勾股定理列方程求出AM的长度.

练习册系列答案
相关题目
13.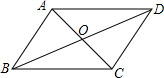 如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
 如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )
如图,?ABCD的对角线AC、BD相交于点O,若AB=5,△OCD的周长为16,则AC与BD的和是( )| A. | 10 | B. | 11 | C. | 12 | D. | 22 |
17. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG=2. 如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由.
如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由. 如果,如果AB∥CD,试猜想α、β、γ之间的关系,并说明理由.
如果,如果AB∥CD,试猜想α、β、γ之间的关系,并说明理由.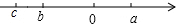 a,b,c在数轴上的位置如图,化简|a+b|+|b+c|-|a-c|-|a+c|.
a,b,c在数轴上的位置如图,化简|a+b|+|b+c|-|a-c|-|a+c|.